|
|
|
To: 7.2 Counter-rotating vortex pair |
We will present numerical results for Reynolds numbers
of 0, 10, 50 and 100.
Because of data available in literature, we
computed the range
![]() .
Note that the maximum value of
.
Note that the maximum value of ![]() by itself is of no relevance to this
flow since there is no inherent length scale; the only important parameter
is the maximum ratio of
by itself is of no relevance to this
flow since there is no inherent length scale; the only important parameter
is the maximum ratio of ![]() to the typical nondimensional area per
computational point. We used a numerical time step
to the typical nondimensional area per
computational point. We used a numerical time step
![]() and we also
repeated all computations at
and we also
repeated all computations at
![]() to verify their
accuracy. As explained in subsection 6.2.3,
we performed redistribution over a neighborhood of radius
to verify their
accuracy. As explained in subsection 6.2.3,
we performed redistribution over a neighborhood of radius
![]() . Where no solution to the redistribution
problem could be found, we added new vortices at a distance
. Where no solution to the redistribution
problem could be found, we added new vortices at a distance
![]() .
We used the vortex core (6.3)
of size
.
We used the vortex core (6.3)
of size
![]() in integrating the convection
processes, and the core (6.12)
of size
in integrating the convection
processes, and the core (6.12)
of size
![]() to
to
![]() to evaluate pointwise vorticity values.
The computations were carried out
in 32 bit precision on a VAX4000-300 computer running VMS V6.0.
to evaluate pointwise vorticity values.
The computations were carried out
in 32 bit precision on a VAX4000-300 computer running VMS V6.0.
 |
Other investigations of similar flows have focussed on the
average square radius of the vortex,
![]() ,
which grows as
,
which grows as ![]() .
The redistribution scheme
reproduces this growth exactly due to (4.10),
while in the absence of numerical errors
the vortex blob method preserves it during the convection step
(3.18, 3.19).
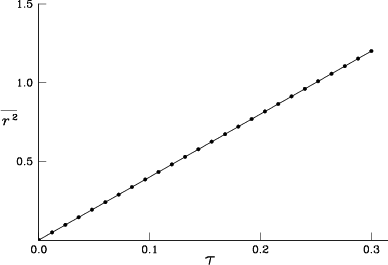
Indeed figure 7.1 shows excellent agreement between the
computed and exact values of
.
The redistribution scheme
reproduces this growth exactly due to (4.10),
while in the absence of numerical errors
the vortex blob method preserves it during the convection step
(3.18, 3.19).
Indeed figure 7.1 shows excellent agreement between the
computed and exact values of
![]() , indicating that
the solution of the redistribution equations and the numerical
integration of convection are accurate. The relative error is of
order
, indicating that
the solution of the redistribution equations and the numerical
integration of convection are accurate. The relative error is of
order ![]() .
.
According to the exact solution, circulation should be preserved; in our
numerical solutions it was preserved to six digits accuracy.
Further, according to the exact solution the mean vortex position should
remain at the origin. In our numerical results for the Stokes flow, it does
so to an accuracy of ![]() .
This error increases to the order of
.
This error increases to the order of ![]() for higher
Reynolds numbers in agreement with the chosen truncation error
in the fast velocity summation scheme [233].
It is clear from existing studies such as
[78,79,155,182]
that such accuracy could not be achieved using
the random walk method with the same number of vortices.
for higher
Reynolds numbers in agreement with the chosen truncation error
in the fast velocity summation scheme [233].
It is clear from existing studies such as
[78,79,155,182]
that such accuracy could not be achieved using
the random walk method with the same number of vortices.
Despite the arbitrary locations of the vortices, it is possible
to obtain accurate pointwise vorticity values.
For example, figure 7.2 compares the numerical vorticity
along a horizontal line with the exact solution.
A close examination shows that since the infinite-order
smoothing function is not entirely positive, it produces very small
negative vorticity at the tail end of the distribution.
The maximum errors at ![]() =0.082 and 0.202 are 0.046 and 0.016 respectively,
which amounts to 0.75% and 0.65% of the maximum vorticity.
Results such as those of Fogelson & Dillon [79]
show clearly that the random walk method cannot achieve such
pointwise accuracy without an excessive number of vortices.
=0.082 and 0.202 are 0.046 and 0.016 respectively,
which amounts to 0.75% and 0.65% of the maximum vorticity.
Results such as those of Fogelson & Dillon [79]
show clearly that the random walk method cannot achieve such
pointwise accuracy without an excessive number of vortices.
Table 7.1 shows the number of vortices and computational times for the fast summation and redistribution parts of the computation. It should be noted that the time needed for convection is increased due to subdivision of the convective time-step: since the flow starts from a concentrated vortex, during the first few time-steps the vortices rotate rapidly about each other. To limit the corresponding numerical errors, the early convection time steps were subdivided further. For example, at Reynolds number 50, the first convection step was subdivided into 50 equal parts. The subdivision was then decreased inversely proportional to the time-step number. Since the number of vortices at early times is very small, the additional amount of work is limited.
As discussed at the end of subsection 6.2.1, the diffusion time may be greatly reduced for Stokes flow, and most likely also for other Reynolds numbers, by not solving the redistribution equations from scratch each time-step. As discussed at the end of subsection 6.2.3, the number of vortices at high Reynolds number may be reduced by some form of regeneration of the vortex distribution. This was not done here.
In any case, table 7.1 shows very clearly that the computational time for diffusion is acceptable even using our simple initial approaches. To put this in perspective, note that it requires 16 times more computational effort to resolve spatial scales that are only smaller by a factor 2. In addition, we may note that our method resolves smaller scales than competing vortex methods for the same number of vortices (see section 9.1).