| A New Mesh-Free Vortex Method |
|
Shankar Subramaniam |
|
3.2 Vortex methods for viscous flows
For Newtonian viscous flows, the vorticity equation
(2.4) is
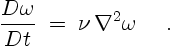 |
(3.17) |
To solve (3.17) numerically, we use the viscous splitting
algorithm mentioned in the introduction of this chapter.
Mathematically, this algorithm is expressed by splitting each
time-step into a convection step and a diffusion step as follows
(Chorin et al. [53]):
Convection step:
Diffusion step:
In the above equations, 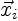 and
and 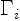 are the position and
circulation of vortex
are the position and
circulation of vortex 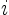 respectively;
respectively;
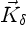 is the velocity
kernel
is the velocity
kernel
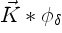 ;
and
;
and 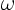 is the smooth vorticity distribution represented by the
vortices
is the smooth vorticity distribution represented by the
vortices 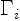 .
.
A number of theoretical studies have shown that the velocity field
from the viscous splitting algorithm converges to the velocity field
of the Navier-Stokes equations. Beale & Majda [19]
have shown the convergence for flows in free space. Ying [251]
and Beale & Greengard [15] showed convergence
for flows over solid boundaries.