| A New Mesh-Free Vortex Method |
|
Shankar Subramaniam |
|
3.1 Vortex methods for inviscid flows
For an inviscid fluid, the vorticity equation (2.4) in the
previous chapter reduces to,
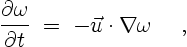 |
(3.1) |
in which the vorticity 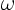 is the curl of the flow velocity.
The above equation can also be derived as the curl of the Euler equations
[14].
Following a fluid particle, (3.1) becomes [14],
is the curl of the flow velocity.
The above equation can also be derived as the curl of the Euler equations
[14].
Following a fluid particle, (3.1) becomes [14],
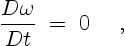 |
(3.2) |
in which the time derivative 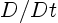 keeps the fluid particle constant.
In other words, according to (3.2) the vorticity of a fluid
particle does not change in time. Based on Low's [137] observation,
the fluid containing vorticity can be divided into
distinct fluid particles of constant vorticity; then the motion of these fluid
particles determines the evolution of the vorticity.
To describe the motion of the fluid particles mathematically,
following Anderson & Greengard [11], and
Hou [109] for example,
let
keeps the fluid particle constant.
In other words, according to (3.2) the vorticity of a fluid
particle does not change in time. Based on Low's [137] observation,
the fluid containing vorticity can be divided into
distinct fluid particles of constant vorticity; then the motion of these fluid
particles determines the evolution of the vorticity.
To describe the motion of the fluid particles mathematically,
following Anderson & Greengard [11], and
Hou [109] for example,
let
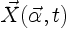 be the
position of a fluid particle at any time
be the
position of a fluid particle at any time 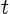 , where
, where 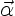 is the initial location of the particle. Following the fluid
particles, the vorticity distribution at any time can be obtained
from the initial vorticity distribution as
is the initial location of the particle. Following the fluid
particles, the vorticity distribution at any time can be obtained
from the initial vorticity distribution as
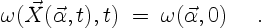 |
(3.3) |
The path of the particle is obtained from the following equations:
where
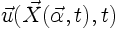 is the velocity of the fluid
particle. The velocity in (3.4) can be obtained from
(3.6) using (2.16)
in the previous chapter,
is the velocity of the fluid
particle. The velocity in (3.4) can be obtained from
(3.6) using (2.16)
in the previous chapter,
In the above equation (3.7), the integration
is over all space and 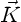 is given by
is given by
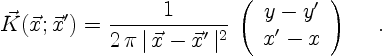 |
(3.8) |
McGrath [150], and Marchioro & Pulvirenti [143]
have shown that the velocity and vorticity obtained from
solving (3.4) through (3.7)
is a weak solution of Euler equation (3.1).
The equations (3.4) through (3.7)
can be solved numerically using vortex methods.
In a computation,
the vorticity distribution can be represented by a collection of
discrete amounts of vorticity (vortices).
A simple way to create vortices is to divide the flow region
into small fluid particles.
To each fluid particle we assign a vortex; the circulation of the
vortex is taken to be either the total circulation
(integrated vorticity) of the fluid particle
or the product of a representative vorticity value of the
fluid particle and the area occupied by the fluid particle [106].
Using the vortices created, the vorticity
distribution is mathematically approximated by
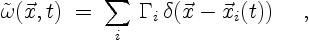 |
(3.9) |
where 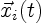 is the location of vortex
is the location of vortex 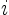 at time
at time 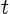 ;
;
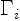 is the circulation or the strength of the vortex;
and
is the circulation or the strength of the vortex;
and 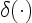 is the Dirac delta function
[11,109,184].
The vortices in (3.9) are called point vortices since they are
represented by delta functions.
Rosenhead [184] was probably the first to compute
the evolution of vorticity in an inviscid flow using a point vortex method.
He investigated the instability of a vortex sheet
numerically by representing the vortex sheet by a collection
of vortices of prescribed strengths. The motion of these vortices was
then used to describe the evolution of the vortex sheet.
is the Dirac delta function
[11,109,184].
The vortices in (3.9) are called point vortices since they are
represented by delta functions.
Rosenhead [184] was probably the first to compute
the evolution of vorticity in an inviscid flow using a point vortex method.
He investigated the instability of a vortex sheet
numerically by representing the vortex sheet by a collection
of vortices of prescribed strengths. The motion of these vortices was
then used to describe the evolution of the vortex sheet.
In equation (3.9), the vorticity distribution
at any time depends on the path 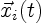 of the vortices.
To find the path of the point vortices, we first substitute
(3.9) for the vorticity in
(3.7) to obtain the velocity; and then, using this velocity
in (3.4) we obtain a system of ordinary differential equations
for the paths of the vortices,
of the vortices.
To find the path of the point vortices, we first substitute
(3.9) for the vorticity in
(3.7) to obtain the velocity; and then, using this velocity
in (3.4) we obtain a system of ordinary differential equations
for the paths of the vortices,
where
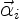 is the initial location of vortex
is the initial location of vortex 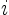 .
Goodman, Hou and Lowengrub [91] have shown that the
solution
.
Goodman, Hou and Lowengrub [91] have shown that the
solution 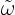 of the point vortex method converges to the
solution
of the point vortex method converges to the
solution 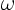 of the vorticity equation
(3.1) for any finite time if the vortices are
initially uniformly spaced. Hou [109] has given a survey of the
convergence analysis for point vortex methods for both two and
three-dimensional flows.
of the vorticity equation
(3.1) for any finite time if the vortices are
initially uniformly spaced. Hou [109] has given a survey of the
convergence analysis for point vortex methods for both two and
three-dimensional flows.
However, a numerical difficulty with point vortex methods is that the
velocity field becomes unbounded if any two vortices come very
close to each other [11].
Beale & Majda [17] have shown that there is another difficulty
with point vortex methods: the computed velocity field is
unreliable at locations other than vortex positions.
To handle the above numerical difficulties of the point vortex methods
Chorin [54] suggested using ``vortex blobs", instead of
point vortices. A vortex blob is obtained by spreading the circulation
of a point vortex over a chosen small area that is called the vortex core.
Using the vortex blobs, the vorticity field is approximated by
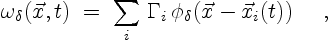 |
(3.11) |
where the function 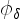 describes the vorticity distribution
in the vortex core; and the
subscript
describes the vorticity distribution
in the vortex core; and the
subscript 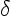 represents the characteristic size of the vortex core.
The function
represents the characteristic size of the vortex core.
The function 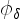 is also known as smoothing function,
core function or core shape [11].
Mathematically, (3.11) can be interpreted as the result of
convolving the delta-function approximation of the
the vorticity (3.9) with the smoothing function
is also known as smoothing function,
core function or core shape [11].
Mathematically, (3.11) can be interpreted as the result of
convolving the delta-function approximation of the
the vorticity (3.9) with the smoothing function
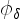 ; that is,
; that is,
The smoothing function in (3.11) is usually chosen
[11,126,178] to be of form
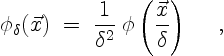 |
(3.13) |
such that 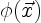 integrates to unity. In computations,
Leonard [126] for example,
integrates to unity. In computations,
Leonard [126] for example,
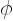 is taken to be an axisymmetric smoothing
function for simplicity in evaluating the velocity field.
Beale and Majda [17] give various properties of
smoothing functions of the form (3.13);
they also show how to construct
such functions, for both two and three-dimensions,
to approximate the vorticity to high orders of accuracy.
Winckelmans and Leonard [247] also give a list of
smoothing functions in both two and three-dimensions.
Beale & Majda [17], Perlman [172], and
Daleh [70]
have studied the choice of smoothing function and core size based on the
errors in the computed velocity and vorticity fields.
They conclude that the core size
is taken to be an axisymmetric smoothing
function for simplicity in evaluating the velocity field.
Beale and Majda [17] give various properties of
smoothing functions of the form (3.13);
they also show how to construct
such functions, for both two and three-dimensions,
to approximate the vorticity to high orders of accuracy.
Winckelmans and Leonard [247] also give a list of
smoothing functions in both two and three-dimensions.
Beale & Majda [17], Perlman [172], and
Daleh [70]
have studied the choice of smoothing function and core size based on the
errors in the computed velocity and vorticity fields.
They conclude that the core size 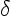 of the vortices must be much
larger than the average spacing
of the vortices must be much
larger than the average spacing 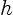 between the vortices;
in most work the
core size is taken to be
between the vortices;
in most work the
core size is taken to be 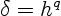 , where
, where 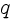 is well less than one.
is well less than one.
In (3.11), the vorticity distribution
at any time depends on the path 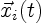 of the vortex blobs.
To find this path, we first need to find the velocity
due to the vortex blobs; to do that, we substitute the vorticity given
by (3.12) for the vorticity in (3.7) to obtain,
of the vortex blobs.
To find this path, we first need to find the velocity
due to the vortex blobs; to do that, we substitute the vorticity given
by (3.12) for the vorticity in (3.7) to obtain,
Evaluating the convolution (3.14) can be made simpler if
we rewrite it using (3.9) as
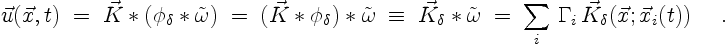 |
(3.15) |
In the above summation the velocity kernel
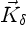 does not depend on the particular vorticity field. It
can often be found explicitly for a proper choice of the axisymmetric
smoothing function
does not depend on the particular vorticity field. It
can often be found explicitly for a proper choice of the axisymmetric
smoothing function 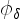 [17,247].
[17,247].
To find the velocity of all the vortices using (3.15),
the computational effort is 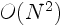 , where
, where 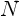 is the number of vortices.
A number of fast algorithms have been developed to do reduce the
effort to
is the number of vortices.
A number of fast algorithms have been developed to do reduce the
effort to
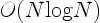 operations
[2,5,10,36,74,75,97,217,233].
operations
[2,5,10,36,74,75,97,217,233].
We can now use the velocity given by (3.15) in
(3.4) to find the path of the vortex blobs as
where
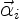 is the initial location of
vortex blob
is the initial location of
vortex blob 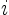 .
The convergence of the solution obtained from the above vortex blob method
to that of the vorticity equation (3.1) has been established
by Hald [106,107],
Beale & Majda [18], Raviart [180],
and Anderson & Greengard [11].
To integrate (3.16),
many numerical schemes use Runge-Kutta time stepping. Anderson & Greengard
[11], and Hald [106] have shown the convergence
of vortex blob schemes that use Runge-Kutta schemes.
.
The convergence of the solution obtained from the above vortex blob method
to that of the vorticity equation (3.1) has been established
by Hald [106,107],
Beale & Majda [18], Raviart [180],
and Anderson & Greengard [11].
To integrate (3.16),
many numerical schemes use Runge-Kutta time stepping. Anderson & Greengard
[11], and Hald [106] have shown the convergence
of vortex blob schemes that use Runge-Kutta schemes.
To summarize, the numerical implementation of vortex methods for inviscid
flows consists of moving the vortices (points or blobs) to new locations
using the equations (3.10) or (3.16) at each time
step of the computation. For viscous flows, in addition to moving the
vortices, the diffusion process must also be represented;
we will discuss that in the next section.
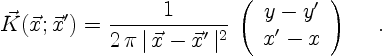
![]() of the vortices.
To find the path of the point vortices, we first substitute
(3.9) for the vorticity in
(3.7) to obtain the velocity; and then, using this velocity
in (3.4) we obtain a system of ordinary differential equations
for the paths of the vortices,
of the vortices.
To find the path of the point vortices, we first substitute
(3.9) for the vorticity in
(3.7) to obtain the velocity; and then, using this velocity
in (3.4) we obtain a system of ordinary differential equations
for the paths of the vortices,
![]() of the vortex blobs.
To find this path, we first need to find the velocity
due to the vortex blobs; to do that, we substitute the vorticity given
by (3.12) for the vorticity in (3.7) to obtain,
of the vortex blobs.
To find this path, we first need to find the velocity
due to the vortex blobs; to do that, we substitute the vorticity given
by (3.12) for the vorticity in (3.7) to obtain,
![]() , where
, where ![]() is the number of vortices.
A number of fast algorithms have been developed to do reduce the
effort to
is the number of vortices.
A number of fast algorithms have been developed to do reduce the
effort to
![]() operations
[2,5,10,36,74,75,97,217,233].
operations
[2,5,10,36,74,75,97,217,233].