|
|
|
|
|
Next: 7.2 A parabolic example |
|
The Laplace transform pairs a function of a real coordinate, call it
![]() , with
, with ![]() , with a different function of a complex
coordinate
, with a different function of a complex
coordinate ![]() :
:
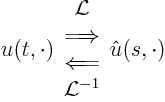
Use tables to find the equations satisfied by ![]() from these
satisfied by
from these
satisfied by ![]() . Solve for
. Solve for ![]() and look up the corresponding
and look up the corresponding
![]() in the tables.
in the tables.
Table 7.1 lists important properties of the Laplace
transform and table 7.2 gives example Laplace transform
pairs. In the tables, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are constants, normally
positive,
are constants, normally
positive, ![]() is a natural number, and
is a natural number, and
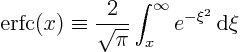
In many cases, ![]() is physically time, since time is most likely
to satisfy the constraints
is physically time, since time is most likely
to satisfy the constraints ![]() and coefficients independent
of
and coefficients independent
of ![]() . Also, the Laplace transform likes initial conditions at
. Also, the Laplace transform likes initial conditions at
![]() , not boundary conditions at both
, not boundary conditions at both ![]() and
and ![]() .
.