2.1 Introduction

The purpose of this section is to introduce the Green’s function ideas.

2.1.1 The one-dimensional Poisson equation

This subsection will consider a very simple problem, the Poisson equation in one-dimensional infinite space. The solution will be obtained using a Green’s function approach.

In general, the Poisson equation reads

$$\nabla^2 u = f$$

where $f$ is a given function and $u$ the unknown to be found. In one-dimensional infinite space that becomes

$$u_{xx} = f(x) \qquad -\infty < x \infty$$

Of course, this equation is trivial to solve. That makes it such a good example to understand the Green’s function approach.

It may be noted that the solution is not quite unique; adding $A+Bx$ to any solution, with $A$ and $B$ constants, produces another solution. Therefore, solving the problem will simply be taken to be finding a solution, whichever one.

Figure 2.1: Chopping a one-dimensional function up into spikes.

Figure 2.1 shows a sketch of an arbitrary given function $f(x)$.

The basic idea of a Green’s function approach is to chop the function into narrow spikes and solve for each spike separately.

Figure 2.2: Contribution of one spike to the solution.

Consider an arbitrary example spike, shown in grey in figure 2.1. Figure 2.2 shows this one spike separately. The solution due to this one spike, call it ${\Delta}u$, is shown in red. The total solution can be obtained by summing the solutions for all the spikes together:

$$u = \sum_{{\rm all spikes}} \Delta u$$

To be sure, solving the problems for the spikes exactly is just as difficult as solving the original problem. But if the spikes are narrow, approximations can be made. Before doing so however, consider the exact solution ${\Delta}u$ in figure 2.2 more closely. Note that the solution is linear everywhere except in the narrow region of the spike. That is because it satisfies the Poisson equation

$$\Delta u_{xx} = \Delta f$$

Now ${\Delta}f$, as shown in green in figure 2.2, is zero everywhere outside the spike region. And if the second derivative of ${\Delta}u$ is zero, then ${\Delta}u$ is linear.

The slope changes from one side of the spike region to the other. In fact, integration of the equation above produces

$$\Delta u_{x,\rm after} - \Delta u_{x,\rm before} = \int_{\rm spike} f(\xi'){ \rm d}\xi'$$

Figure 2.2 took the slopes equal and opposite at both sides

Figure 2.3: Approximation of the spike by an infinitely narrow one.

To approximate this solution, the trick is to replace the actual spike by an infinitely narrow one. That idea is sketched in figure 2.3. Note that for a valid approximation, the change in slope must be the same as that for the exact solution. If the change in slope is different, then there is no way that the approximate solution can meaningfully approximate the exact solution at both sides of the original spike. To be precise, a small error is allowed. It can be seen that it is accurate enough to approximate the exact integral over the spike as

$$\int_{\rm spike} f(\xi'){ \rm d}\xi' \approx f(\xi)\Delta\xi$$

where $\xi$ is the center point of the interval and $\Delta\xi$ is the width of the spike. The infinitely thin spike must produce a slope change equal to that amount.

To formalize the approximation, it is useful to introduce a few new concepts. First of all,

A delta function is defined as an infinitely narrow, infinitely high spike that integrates to 1.

By convention, in one dimension a delta function located at a point $\xi$ is indicated as $\delta(x-\xi)$.

Now the approximate spike in figure 2.3 must integrate to $f(\xi)\Delta\xi$, not 1. So that spike is

$$\delta(x-\xi) f(\xi)\Delta\xi$$

Next

A Green’s function is defined as a solution for a delta function inhomogeneous term.

In one dimension a Green’s function is typically indicated as $G(x;\xi)$ where $\xi$ is the location of the delta function. Since the delta function in figure 2.3 is multiplied by a factor $f(\xi)\Delta\xi$, so is the Green’s function solution.

All that is left to do now is find the Green’s function. That is not difficult. Recall that the change in slope going from one side of the spike to the other must equal the integral of the spike. For a delta function, the integral is 1. So the slope must change by 1. A solution that does that is

$$\fbox{$\displaystyle G_{xx} = \delta(x-\xi) \quad -\inft... ... G(x;\xi) = {\textstyle\frac{1}{2}} \vert x-\xi\vert $} %$$ (2.1)

Indeed, for $x>\xi$, the absolute signs do nothing, so the slope is ${\textstyle\frac{1}{2}}$. For $x<\xi$, the absolute signs produce a change of sign so the slope is $-{\textstyle\frac{1}{2}}$. That makes the total change in slope 1.

In summary, to solve

$$u_{xx} = f(x) \qquad -\infty < x \infty$$

first chop the function $f(x)$ into narrow spikes. Each spike produces an approximate solution

$$\Delta u(x;\xi) \approx G(x;\xi) f(\xi)\Delta\xi = {\textstyle\frac{1}{2}} \vert x - \xi\vert f(\xi)\Delta\xi$$

where $\xi$ is the center point of the spike and $\Delta\xi$ its width. To get the total solution $u(x)$, sum all these approximate solutions together. The following example explores that idea.

Example

Question: Find Green’s function approximations to the solution $u$ of the Poisson problem

$$u_{xx} = -2 x e^{-x^2} \qquad -\infty < x < \infty$$

Solution:

Figure 2.4 shows some results obtained using matlab. First of all, this problem has an exact solution

$$\frac{\sqrt{\pi}}{2} {\rm erf}(x)$$

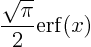
where erf is the so-called error function. This exact solution is indicated by the blue dots in figure 2.4.

Figure 2.4: Green’s function solution of an example one-dimensional Poisson equation.

The question is now, how good is a Green’s function approximation for this problem?

The right hand side in the Poisson problem is negligibly small outside the range $-3<x<3$, so no spikes are needed outside that range. In the top left graph, the interval $-3<x<3$ was chopped up into two “spikes.” Each spike was approximated by a delta function spike at its center as described above. Then the two Green’s function solutions of these spikes were added to give the red solid line. You can see the locations of the delta functions from the kinks in this solution. Obviously, this Green’s function solution is not accurate.

It gets better if the interval $-3<x<3$ is divided up into 5 narrower spikes, and each one is approximated by a delta function spike. The solution for that is shown in the top right graph of figure 2.4. The next graph shows that for 10 spikes, the Green’s function solution is quite close to the exact solution. However, there are still visible kinks at the locations of the delta function spikes. At 20 spikes, the kinks are virtually invisible.

As the example suggests, you get the exact solution to the Poisson problem by letting the width of the spikes become infinitesimal. In that case, summation becomes integration:

$$\fbox{$\displaystyle u_{xx} = f(x) \quad -\infty < x < \... ...tstyle\frac{1}{2}}\vert x-\xi\vert f(\xi){ \rm d}\xi $} %$$ (2.2)

You can verify this solution by splitting the integral into two and integrating by parts. It is somewhat messy to do so, however.

2.1.1 Review Questions

1

Solve the Poisson equation

$$u_{xx} = - 2 \frac{\sinh x}{\cosh^3 x}$$

numerically using Green’s functions.

Solution gf1d-a

2

Show that

$$\tilde u(x) = \int_{\xi =-\infty}^\infty{\textstyle\frac{1}{2}}\vert x-\xi\vert f(\xi){ \rm d}\xi$$

is a solution to

$$u_{xx} = f(x) \quad -\infty < x < \infty$$

You can assume that function $f(\xi)$ becomes zero rapidly at large $\xi$. (If you want, you can assume it is zero beyond some value $\xi_{\rm {max}}$ of $\vert\xi\vert$.)

Solution gf1d-b

2.1.2 More on delta and Green’s functions

Figure 2.5 shows the definition of the one-dimensional Green’s function. Note that the function value of $\delta(x-\xi)$ is zero at all points except at the single point $\xi$. At that single point however, the function value is infinite.

Figure 2.5: Approximate Dirac delta function $\delta_\varepsilon(x-\xi)$ is shown left. The true delta function $\delta(x-\xi)$ is the limit when $\varepsilon$ becomes zero, and is an infinitely high, infinitely thin spike, whose bottom is shown right.

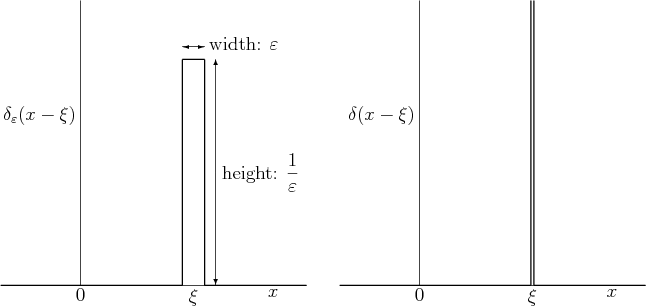Of course, infinite function values are invalid mathematics. The Green’s function is not a properly defined function. The best way to deal with that as an engineer is to mentally not make the delta function infinitely narrow. Instead think of a delta function as an extremely narrow, extremely high spike that integrates to 1. Mathematicians have better but more complicated ways of dealing with the problem, {A.1}.

Usually delta functions are used as inhomogeneous terms in differential equation problems. The solutions to these problems are called Green’s functions. Fortunately, it turns out that while the delta function is not well defined, the Green’s function typically is. In the limit that the width of the delta function becomes zero, the Green’s function stays a perfectly good function.

Like the example of the precious section illustrates, Green’s functions in infinite domains are usually not unique. The most general Green’s function for the Poisson equation in one dimension is

$$G(x;\xi) = {\textstyle\frac{1}{2}} \vert x-\xi\vert + A + B x$$

where $A$ and $B$ are arbitrary constants. The final two terms are a solution of the homogeneous equation.

You would typically like the Green’s function to be zero at large distances. But for the one dimensional Green’s function above, (as well as for the two-dimensional equivalent, for that matter), there is no way to do it. There is no way to choose $A$ and $B$ so that $G$ is zero at both $\pm\infty$. The best you can do is make the derivatives at $\pm\infty$ as small as possible. If $B$ is nonzero, the derivative at either $-\infty$ or $\infty$ is greater than $\frac12$ in magnitude. So you take $B$ zero so that neither derivative exceeds $\frac12$ in magnitude. There is nothing defensible that you can take for the constant $A$, so you take it also zero.

It may be noted that in wave propagation problems, trying to make the wave function as small as possible typically does not work. Instead you take the Green’s function so that at large distances it describes waves that move away to infinity. Green’s functions that describe waves that come in from infinity are physically undesirable.