clear all
Add MCMC codes to path
current_directory = cd;
addpath(strcat(current_directory,'/mcmcstat'));
The following analysis computes two electrostrictive parameters and a residual stress used in estimating changes in stress as a function of changes in the internal electronic state. The results are calculated from prior density functional theory (DFT) calculations. The DFT calculations were computed by incrementing atoms in lead titanate in a prescribed manner to produce changes in polarization about a fixed cubic strain state. This decouples the polarization energy and electrostriction for conducting independent energy and electrostrictive model calibration. More details about this analysis can be found in:
Oates, W., "A Quantum-informed Continuum Model for Ferroelectric Materials," Smart Mater. Struct. v. 23(10), p. 104009, 2014.
The form of the electrostrictive stress components considered for model calibration is
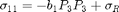
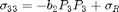
where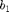 
and 
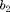are the electrostrictive parameters and 
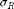is the residual stress that will be calibrated through the Bayesian analysis. In this particular example, polarization 
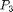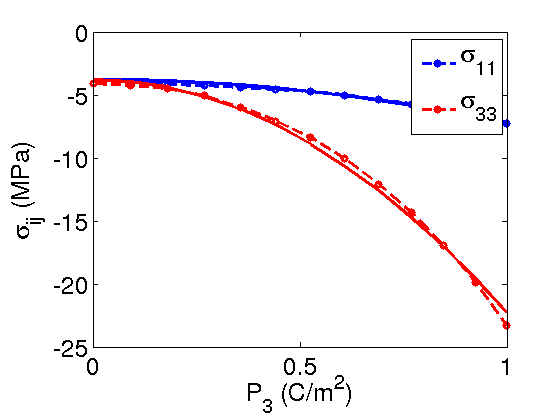
in the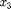 
direction is used which was calculated using the Berry phase approach in the DFT code ABINIT.
Define a function that calculates the sum of squares of error between the DFT stresses and the approximation based on the electrostrictive stress constitutive relation.
ssfun = @coupled_func_Bayesian; model.ssfun = ssfun;
Load and apply variables for the DFT computational results for comparison to the electrostrictive constitutive law.
load DFT_cubic model.N = length(Pnum); data.ydata_s11 = sig11_num; data.ydata_s33 = sig33_num; data.xdata = Pnum; %polarization computed from DFT using the Berry phase approach %define initial guess for electrostrictive parameters b1 = 3.4; %electrostrictive parameter b2 = 18.5; %electrostrictive parameter sigR = -3.8; %residual stress tmin = [b1 b2 sigR]; %Electrostrictive model parameter range and initial guess params = { {'b_1', tmin(1), -20, 20} {'b_2', tmin(2), -20,50} {'\sigma^R', tmin(3), -50,50} };
The next lines of code check the parameters prior to running a parameter estimation using MCMC.
[s11,s33] = coupled_model_Bayesian(tmin,data.xdata); ss = coupled_func_Bayesian(tmin,data); SS = ss/length(data.xdata); %here is the cost calculation figure(1) axes1 = axes('FontSize',20); plot((data.xdata),data.ydata_s11,'bo--','Linewidth',3) hold on plot((data.xdata),data.ydata_s33,'ro--','Linewidth',3) plot((data.xdata),s11,'b-','Linewidth',3) plot((data.xdata),s33,'r-','Linewidth',3) hold off ylabel('\sigma_{ij} (MPa)','FontSize',20) xlabel('P_3 (C/m^2)','FontSize',20) legend('\sigma_{11}','\sigma_{33}') legend1 = legend(axes1,'show'); set(legend1,'EdgeColor',[1 1 1],'YColor',[1 1 1],'XColor',[1 1 1]); variance = sum((data.ydata_s33-s33).^2)/(length(s33-1)); %estimation of the variance based on one %stress component, %s33 %
Bayesian MCMC Statistical analysis
model.S20 = variance/1e3; %estimate of variance based on prior simulation model.N0 = 1; model.N = length(Pnum); options.updatesigma=1; options.method = 'dram'; %this applies the DRAM algorithm options.nsimu = 1000; %run an initial small set of iterations prior to larger run [results, chain, s2chain] = mcmcrun(model,data,params,options); options.nsimu = 5000; %run longer simulations using results from smaller run as %initial conditions [results, chain, s2chain] = mcmcrun(model,data,params,options,results); %
Setting nbatch to 1 Sampling these parameters: name start [min,max] N(mu,s^2) b_1: 3.4 [-20,20] N(0,Inf) b_2: 18.5 [-20,50] N(0,Inf) \sigma^R: -3.8 [-50,50] N(0,Inf) Setting nbatch to 1 Using values from the previous run Sampling these parameters: name start [min,max] N(mu,s^2) b_1: 3.61204 [-20,20] N(0,Inf) b_2: 18.2685 [-20,50] N(0,Inf) \sigma^R: -3.8265 [-50,50] N(0,Inf)
Plot results
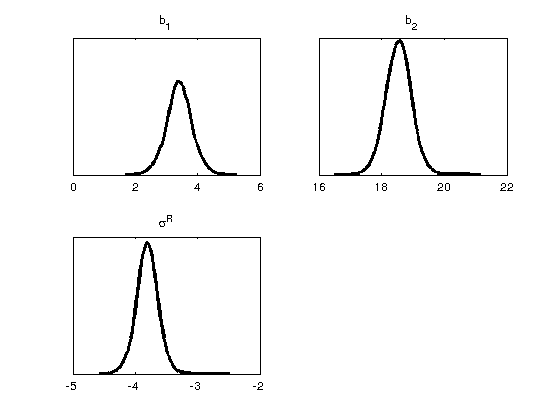
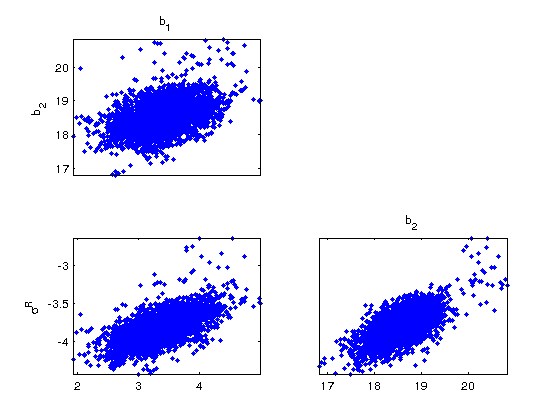
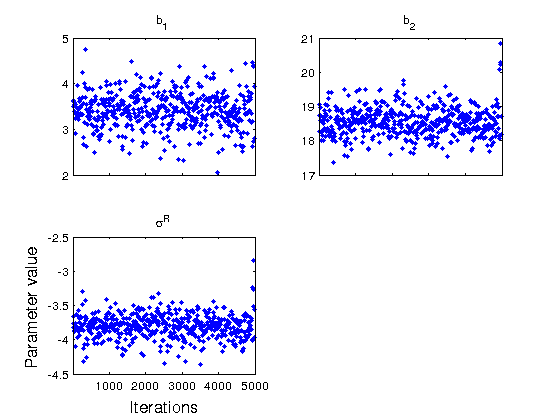
figure(2) mcmcplot(chain,[],results,'denspanel',2); figure(3) mcmcplot(chain,[],results,'pairs'); figure(4); clf mcmcplot(chain,[],results.names,'chainpanel') xlabel('Iterations','Fontsize',14) ylabel('Parameter value','Fontsize',14) chainstats(chain,results) %summary of parameter means, standard deviations, etc.
MCMC statistics, nsimu = 5000
mean std MC_err tau geweke
---------------------------------------------------------------------
b_1 3.4099 0.39673 0.019018 9.8768 0.9796
b_2 18.549 0.41905 0.023486 14.598 0.99524
\sigma^R -3.8048 0.17459 0.009535 11.974 0.99113
---------------------------------------------------------------------
Define a model function that calls the chains for error propagation. Plot the error propagation for both stress components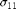 
$ (s11) and 
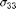$ (s33).
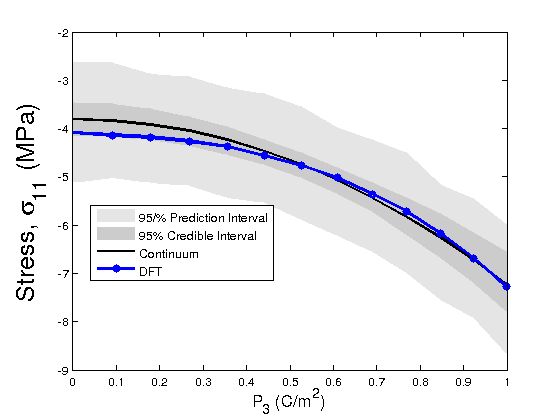
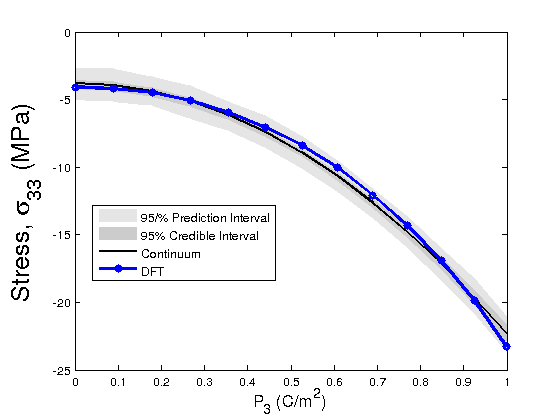
modelfun1 = @(d,th)coupled_model_predict_s11(th,d); %for stress component s11 %The following lines of code propagate the posterior densities of %parameters to determine prediction and credible intervals of the Landau %energy with respect to the DFT energy in light of the Bayesian statistics nsample = 500; out = mcmcpred(results,chain,s2chain,data.xdata,modelfun1,nsample); figure(5) modelout = mcmcpredplot(out); %,data hold on plot(data.xdata,data.ydata_s11,'bo-','linewidth',3) hold off xlabel('P_{3} (C/m^2)','Fontsize',14); ylabel('Stress, \sigma_{11} (MPa)','FontSize',20) legend('95/% Prediction Interval','95% Credible Interval','Continuum','DFT','Location','Best') %Define a model function that calls the chains for error propagation modelfun1 = @(d,th)coupled_model_predict_s33(th,d); %for stress component s_33 %The following lines of code propagate the posterior densities of %parameters to determine prediction and credible intervals of the Landau %energy with respect to the DFT energy in light of the Bayesian statistics nsample = 500; out = mcmcpred(results,chain,s2chain,data.xdata,modelfun1,nsample); figure(6) modelout = mcmcpredplot(out); %,data hold on plot(data.xdata,data.ydata_s33,'bo-','linewidth',3) hold off xlabel('P_{3} (C/m^2)','Fontsize',14); ylabel('Stress, \sigma_{33} (MPa)','FontSize',20) legend('95/% Prediction Interval','95% Credible Interval','Continuum','DFT','Location','Best')
