| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
3.3 The Operators of Quantum Mechanics
The numerical quantities that the old Newtonian physics uses, (position,
momentum, energy, ...), are just shadows
of what
really describes nature: operators. The operators described in this
section are the key to quantum mechanics.
As the first example, while a mathematically precise value of the
position 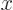 of a particle never exists, instead there is an
of a particle never exists, instead there is an 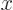 -position operator
-position operator 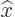 . It turns the wave
function
. It turns the wave
function 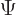 into
into 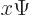 :
:
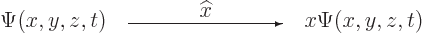 |
(3.3) |
The operators 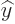 and
and 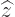 are defined similarly as
are defined similarly as 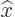 .
.
Instead of a linear momentum 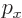

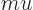 , there is an
, there is an 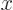 -momentum operator
-momentum operator
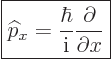 |
(3.4) |
that turns 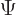 into its
into its 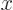 -derivative:
-derivative:
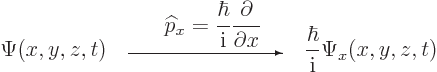 |
(3.5) |
The constant 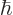 is called “Planck's constant.” (Or rather, it is Planck's original
constant
is called “Planck's constant.” (Or rather, it is Planck's original
constant 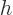 divided by
divided by 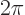 .) If it would have been zero,
all these troubles with quantum mechanics would not occur. The blobs
would become points. Unfortunately,
.) If it would have been zero,
all these troubles with quantum mechanics would not occur. The blobs
would become points. Unfortunately, 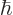 is very small, but
nonzero. It is about 10
is very small, but
nonzero. It is about 10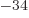 kg m
kg m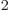 /s.
/s.
The factor 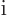 in
in 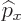 makes it a Hermitian operator (a proof
of that is in derivation {D.9}). All operators reflecting
macroscopic physical quantities are Hermitian.
makes it a Hermitian operator (a proof
of that is in derivation {D.9}). All operators reflecting
macroscopic physical quantities are Hermitian.
The operators 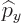 and
and 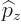 are defined similarly as
are defined similarly as 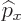 :
:
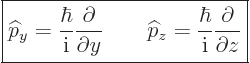 |
(3.6) |
The kinetic energy operator 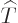 is:
is:
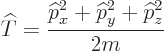 |
(3.7) |
Its shadow is the Newtonian notion that the kinetic energy equals:
This is an example of the “Newtonian analogy”: the relationships between the different
operators in quantum mechanics are in general the same as those
between the corresponding numerical values in Newtonian physics.
But since the momentum operators are gradients, the actual
kinetic energy operator is, from the momentum operators above:
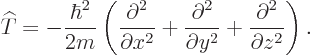 |
(3.8) |
Mathematicians call the set of second order derivative operators in
the kinetic energy operator the Laplacian
, and
indicate it by  :
:
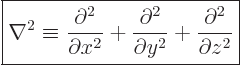 |
(3.9) |
In those terms, the kinetic energy operator can be written more
concisely as:
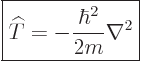 |
(3.10) |
Following the Newtonian analogy once more, the total energy operator, indicated by 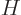 , is the the sum of the
kinetic energy operator above and the potential energy operator
, is the the sum of the
kinetic energy operator above and the potential energy operator 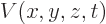 :
:
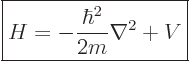 |
(3.11) |
This total energy operator 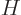 is called the Hamiltonian and it is very important. Its eigenvalues are
indicated by
is called the Hamiltonian and it is very important. Its eigenvalues are
indicated by 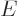 (for energy), for example
(for energy), for example 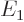 ,
, 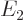 ,
,
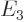 , ...with:
, ...with:
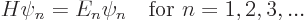 |
(3.12) |
where 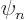 is eigenfunction number
is eigenfunction number 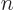 of the Hamiltonian.
of the Hamiltonian.
It is seen later that in many cases a more elaborate numbering of the eigenvalues and eigenvectors of the Hamiltonian is
desirable instead of using a single counter 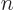 . For example,
for the electron of the hydrogen atom, there is more than one
eigenfunction for each different eigenvalue
. For example,
for the electron of the hydrogen atom, there is more than one
eigenfunction for each different eigenvalue 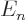 , and
additional counters
, and
additional counters 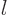 and
and 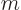 are used to distinguish them. It is
usually best to solve the eigenvalue problem first and decide on how
to number the solutions afterwards.
are used to distinguish them. It is
usually best to solve the eigenvalue problem first and decide on how
to number the solutions afterwards.
(It is also important to remember that in the literature, the Hamiltonian
eigenvalue problem is commonly referred to as the
time-independent Schrödinger equation.
However, this
book prefers to reserve the term Schrödinger equation for the
unsteady evolution of the wave function.)
Key Points

- Physical quantities correspond to operators in quantum mechanics.

- Expressions for various important operators were given.

- Kinetic energy is in terms of the so-called Laplacian operator.

- The important total energy operator, (kinetic plus potential
energy,) is called the Hamiltonian.
![]()
![]() -
-![]() .
.![]()
![]() :
:![]()
![]()
![]() ,
,![]() -
-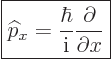
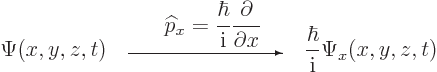
![]()
![]()
![]()
![]()
![]() :
: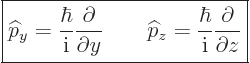
![]()
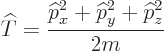
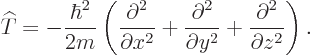
![]() :
: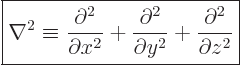
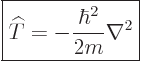
![]() ,
,![]() :
: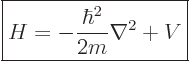
![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]() .
.![]() ,
,![]()
![]()