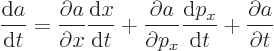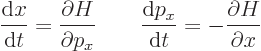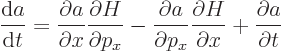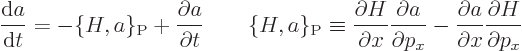| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
A.12 Heisenberg picture
This book follows the formulation of quantum mechanics as developed by
Schrödinger. However, there is another, earlier, formulation due to
Heisenberg. This subsection gives a brief description so that you are
aware of it when you run into it in literature.
In the Schrödinger picture, physical observables like position and
momentum are represented by time-independent operators. The time
dependence is in the wave function. This is somewhat counterintuitive
because classically position and momentum are time dependent
quantities. The Heisenberg picture removes the time dependence from
the wave function and absorbs it into the operator.
To see how that works out, consider first the general form of the wave
function. It can be written as
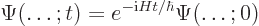 |
(A.37) |
where the exponential of an operator is defined through its Taylor
series:
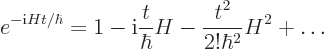 |
(A.38) |
(To check the above expression for the wave function, take the initial
wave function to be any energy eigenfunction of energy 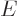 . You
get the correct
. You
get the correct 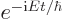 time dependence, chapter
7.1.2. Every
time dependence, chapter
7.1.2. Every 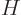 becomes an
becomes an 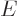 . And if the
expression works for any eigenfunction, it works for all their
combinations too. That means that it works for any wave function,
because the eigenfunctions are complete. To be sure, the above form
of the wave function applies only if the Hamiltonian is independent of
time. Even if it is not, the transformation from the initial wave
function
. And if the
expression works for any eigenfunction, it works for all their
combinations too. That means that it works for any wave function,
because the eigenfunctions are complete. To be sure, the above form
of the wave function applies only if the Hamiltonian is independent of
time. Even if it is not, the transformation from the initial wave
function 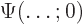 to a later one
to a later one 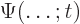 still
remains a “unitary” one; one that keeps the wave function normalized. But
then you will need to use the Schrödinger equation directly to figure out
the time dependence.)
still
remains a “unitary” one; one that keeps the wave function normalized. But
then you will need to use the Schrödinger equation directly to figure out
the time dependence.)
Now consider an arbitrary Schrödinger operator 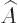 . The
physical effects of the operator can be characterized by inner
products, as in
. The
physical effects of the operator can be characterized by inner
products, as in
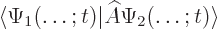 |
(A.39) |
Such a dot product tells you what amount of a wave function 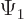 is produced by applying the operator on a wave function
is produced by applying the operator on a wave function
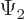 . Knowing these inner products for all wave functions
is equivalent to knowing the operator.
. Knowing these inner products for all wave functions
is equivalent to knowing the operator.
If the time-dependent exponentials are now peeled off 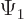 and
and
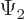 and absorbed into the operator, you get the time-dependent
Heisenberg operator
and absorbed into the operator, you get the time-dependent
Heisenberg operator
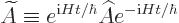 |
(A.40) |
Heisenberg operators will be indicated with a tilde instead of a hat.
Note that the argument of the first exponential changed sign because
it was taken to the other side of the inner product.
The operator 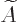 depends on time. To see how it evolves,
differentiate the product with respect to time:
depends on time. To see how it evolves,
differentiate the product with respect to time:
The first and third terms can be recognized as a multiple of the
commutator of 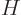 and
and 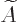 , while the middle term is
the Heisenberg version of the time derivative of
, while the middle term is
the Heisenberg version of the time derivative of 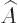 ,
in case
,
in case 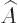 does happen to depend on time. So the evolution
equation for the Heisenberg operator becomes
does happen to depend on time. So the evolution
equation for the Heisenberg operator becomes
![\begin{displaymath}
\frac{{\rm d}\widetilde A}{{\rm d}t} = \frac{{\rm i}}{\hbar...
...}H t/\hbar}
\left[H,\widehat A\right] e^{-{\rm i}H t/\hbar} %
\end{displaymath}](img3870.gif) |
(A.41) |
(Note that there is no difference between the Hamiltonians
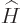 and
and 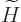 because
because 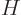 commutes with itself,
hence with its exponentials.)
commutes with itself,
hence with its exponentials.)
For example, consider the Schrödinger 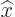 position and
position and 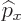 linear
momentum operators of a particle. These do not depend on time. Using
the commutators as figured out in chapter 7.2.1, the
corresponding Heisenberg operators evolve as:
linear
momentum operators of a particle. These do not depend on time. Using
the commutators as figured out in chapter 7.2.1, the
corresponding Heisenberg operators evolve as:
Those have the exact same form as the equations for the classical
position and momentum of the particle.
In fact, the equivalent of the general equation (A.41) is
also found in classical physics: it is derived in advanced mechanics,
with the so-called “Poisson bracket” taking the place of the commutator. As a
simple example, consider one-dimensional motion of a particle. Any
variable 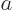 that depends on the position and linear momentum of the
particle, and maybe also explicitly on time, has a time derivative
given by
that depends on the position and linear momentum of the
particle, and maybe also explicitly on time, has a time derivative
given by
according to the total differential of calculus. And from the
classical Hamiltonian
it is seen that the time derivatives of position and momentum obey
the classical “Hamiltonian dynamics”
Substituting this into the time derivative of 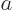 gives
gives
The first two terms in the right hand side are by definition minus the
Poisson bracket 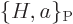 , so
, so
Note that the Poisson bracket, like the commutator, is antisymmetric
under exchange of 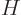 and
and 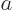 . Apparently, formally identifying
the Poisson bracket with the commutator divided by
. Apparently, formally identifying
the Poisson bracket with the commutator divided by 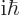 brings
you from classical mechanics to Heisenberg’s quantum mechanics.
brings
you from classical mechanics to Heisenberg’s quantum mechanics.
More generally, the classical Hamiltonian can depend on multiple and
non-Cartesian coordinates, generically called “generalized coordinates.” In that case, in the Poisson bracket
you must sum over all generalized coordinates and their associated
so-called “canonical” momenta. For a Cartesian position coordinate, the
canonical momentum is the corresponding linear momentum. For an
angular coordinate, it is the corresponding angular momentum. In
general, using the so-called Lagrangian formulation usually covered in
an engineering education, and otherwise found in addendum
{A.1}, the canonical momentum is the derivative of
the Lagrangian with respect to the time derivative of the coordinate.
The bottom line is that the Heisenberg equations are usually not easy
to solve unless you return to the Schrödinger picture by peeling off
the time dependence. In relativistic applications however, time joins
space as an additional coordinate, and the Heisenberg picture becomes
more helpful. It can also make it easier to identify the
correspondence between classical equations and the corresponding
quantum operators.
Key Points

- In the Heisenberg picture, operators evolve in time just like
their physical variables do in classical physics.
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]() .
.![]()
![]()
![]()
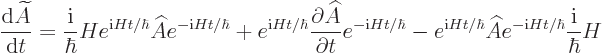
![]()
![]()
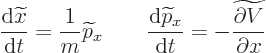
![]()