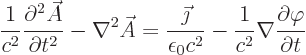| Quantum Mechanics for Engineers |
|
© Leon van Dommelen |
|
A.37 Maxwell’s wave equations
This note derives the wave equations satisfied by electromagnetic
fields. The derivation will use standard formulae of vector analysis,
as found in, for example, [41, 20.35-45].
The starting point is Maxwell’s equations for the electromagnetic
field in vacuum:
Here 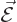 is the electric field,
is the electric field, 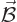 the magnetic field,
the magnetic field,
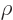 the charge density,
the charge density, 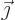 the current density,
the current density, 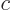 the
constant speed of light, and
the
constant speed of light, and 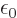 is a constant called the
permittivity of space. The charge and current densities are related
by the continuity equation
is a constant called the
permittivity of space. The charge and current densities are related
by the continuity equation
To get a wave equation for the electric field, take the curl,
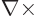 , of (3) and apply the standard vector identity
(D.1), (1) and (4) to get
, of (3) and apply the standard vector identity
(D.1), (1) and (4) to get
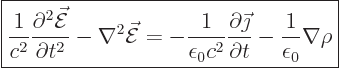 |
(A.235) |
Similarly, for the magnetic field take the curl of (4) and use (2) and
(3) to get
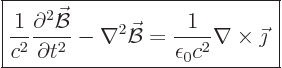 |
(A.236) |
These are uncoupled inhomogeneous wave equations for the components of
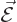 and
and 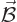 , for given charge and current densities.
According to the theory of partial differential equations, these
equations imply that effects propagate no faster than the speed of
light. You can also see the same thing pretty clearly from the fact
that the homogeneous wave equation has solutions like
, for given charge and current densities.
According to the theory of partial differential equations, these
equations imply that effects propagate no faster than the speed of
light. You can also see the same thing pretty clearly from the fact
that the homogeneous wave equation has solutions like
which are waves that travel with speed 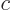 in the
in the 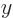 -direction.
-direction.
The wave equations for the potentials 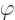 and
and 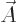 are next.
First note from (2) that the divergence of
are next.
First note from (2) that the divergence of 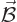 is zero. Then vector
calculus says that it can be written as the curl of some vector. Call
that vector
is zero. Then vector
calculus says that it can be written as the curl of some vector. Call
that vector 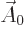 .
.
Next define
Plug this into (3) to show that the curl of 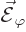 is zero.
Then vector calculus says that it can be written as minus the gradient
of a scalar. Call this scalar
is zero.
Then vector calculus says that it can be written as minus the gradient
of a scalar. Call this scalar 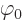 . Plug that into the
expression above to get
. Plug that into the
expression above to get
Next, note that if you define modified versions 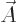 and
and 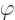 of
of 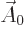 and
and 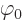 by setting
by setting
where 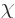 is any arbitrary function of
is any arbitrary function of 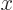 ,
, 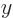 ,
,
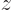 , and
, and 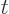 , then still
since the curl of a gradient is always zero, and
because the two
, then still
since the curl of a gradient is always zero, and
because the two 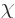 terms drop out against each other.
terms drop out against each other.
The fact that 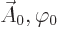 and
and 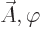 produce the
same physical fields is the famous
produce the
same physical fields is the famous gauge property
of
the electromagnetic field.
Now you can select 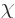 so that
so that
That is known as the “Lorenz condition.” A corresponding gauge function is a
“Lorenz gauge.”
To find the gauge function 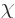 that produces this condition, plug
the definitions for
that produces this condition, plug
the definitions for 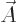 and
and 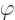 in terms of
in terms of 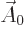 and
and 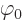 into the left hand side of the Lorentz condition.
That produces, after a change of sign,
into the left hand side of the Lorentz condition.
That produces, after a change of sign,
That is a second order inhomogeneous wave equation for 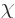 .
.
Now plug the expressions (6) and (7) for 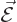 and
and 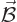 in
terms of
in
terms of 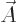 and
and 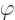 into the Maxwell’s equations.
Equations (2) and (3) are satisfied automatically. From (2),
after using (8),
into the Maxwell’s equations.
Equations (2) and (3) are satisfied automatically. From (2),
after using (8),
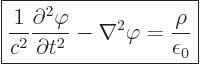 |
(A.237) |
From (4), after using (8),
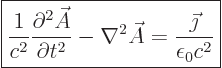 |
(A.238) |
You can still select the two initial conditions for 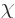 . The
smart thing to do is select them so that
. The
smart thing to do is select them so that 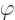 and its time
derivative are zero at time zero. In that case, if there is no charge
density,
and its time
derivative are zero at time zero. In that case, if there is no charge
density, 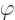 will stay zero for all time. That is because its
wave equation is then homogeneous. The Lorenz condition will then
ensure that
will stay zero for all time. That is because its
wave equation is then homogeneous. The Lorenz condition will then
ensure that 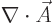 is zero too.
is zero too.
Instead of the Lorenz condition, you could select 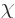 to make
to make
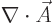 zero. That is called the “Coulomb gauge” or “transverse gauge” or “transverse gauge.” It requires that
zero. That is called the “Coulomb gauge” or “transverse gauge” or “transverse gauge.” It requires that 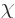 satisfies the
Poisson equation
satisfies the
Poisson equation
Then the governing equations become
Note that 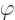 now satisfies a purely spatial Poisson equation.
now satisfies a purely spatial Poisson equation.
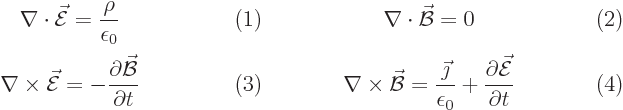
![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
![]() .
.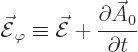

![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
![]()