6.2 The Sin­gle-Par­ti­cle States

As the pre­vi­ous sec­tion noted, the ob­jec­tive is to un­der­stand sys­tems of non­in­ter­act­ing par­ti­cles stuck in a closed, im­pen­e­tra­ble, box. To do so, the key ques­tion is what are the sin­gle-par­ti­cle quan­tum states, or en­ergy eigen­func­tions, for the par­ti­cles. They will be dis­cussed in this sec­tion.

The box will be taken to be rec­tan­gu­lar, with its sides aligned with the co­or­di­nate axes. The lengths of the sides of the box will be in­di­cated by $\ell_x$, $\ell_y$, and $\ell_z$ re­spec­tively.

The sin­gle-par­ti­cle en­ergy eigen­func­tions for such a box were de­rived in chap­ter 3.5 un­der the guise of a pipe with a rec­tan­gu­lar cross sec­tion. The sin­gle-par­ti­cle en­ergy eigen­func­tions are:

$$\fbox{$\displaystyle \pp{n_xn_yn_z}/{\skew0\vec r}/// = \... ...c{8}{{\cal V}}}\; \sin (k_x x) \sin (k_y y) \sin (k_z z) $} %$$ (6.2)

Here ${\cal V}$ $\vphantom0\raisebox{1.5pt}{$=$}$ $\ell_x\ell_y\ell_z$ is the vol­ume of the box. The “wave num­bers” $k_x$, $k_y$, and $k_z$ take the val­ues:

$$\fbox{$\displaystyle k_x = n_x \frac{\pi}{\ell_x}\quad k_... ..._y \frac{\pi}{\ell_y}\quad k_z = n_z \frac{\pi}{\ell_z} $} %$$ (6.3)

where $n_x$, $n_y$, and $n_z$ are nat­ural num­bers. Each set of three nat­ural num­bers $n_x,n_y,n_z$ gives one sin­gle-par­ti­cle eigen­func­tion. In par­tic­u­lar, the sin­gle-par­ti­cle eigen­func­tion of low­est en­ergy is $\pp{111}////$, hav­ing $n_x$ $\vphantom0\raisebox{1.5pt}{$=$}$ $n_y$ $\vphantom0\raisebox{1.5pt}{$=$}$ $n_z$ $\vphantom0\raisebox{1.5pt}{$=$}$ 1.

Fig­ure 6.1: Al­lowed wave num­ber vec­tors, left, and en­ergy spec­trum, right.

How­ever, the pre­cise form of the eigen­func­tions is not re­ally that im­por­tant here. What is im­por­tant is how many there are and what en­ergy they have. That in­for­ma­tion can be sum­ma­rized by plot­ting the al­lowed wave num­bers in a $k_x,k_y,k_z$ axis sys­tem. Such a plot is shown in the left half of fig­ure 6.1.

Each point in this wave num­ber space cor­re­sponds to one spa­tial sin­gle-par­ti­cle state. The co­or­di­nates $k_x$, $k_y$, and $k_z$ give the wave num­bers in the three spa­tial di­rec­tions. In ad­di­tion, the dis­tance $k$ from the ori­gin in­di­cates the sin­gle-par­ti­cle en­ergy. More pre­cisely, the sin­gle par­ti­cle en­ergy is

$$\fbox{$\displaystyle {\vphantom' E}^{\rm p}= \frac{\hbar^2}{2m} k^2 \qquad k \equiv \sqrt{k_x^2 + k_y^2 + k_z^2} $} %$$ (6.4)

The en­ergy is there­fore just a con­stant times the square of this dis­tance. (The above ex­pres­sion for the en­ergy can be ver­i­fied by ap­ply­ing the ki­netic en­ergy op­er­a­tor on the given sin­gle-par­ti­cle wave func­tion.)

One more point must be made. The sin­gle-par­ti­cle en­ergy eigen­func­tions de­scribed above are spa­tial states. Par­ti­cles with nonzero spin, which in­cludes all fermi­ons, can ad­di­tion­ally have dif­fer­ent spin in what­ever is cho­sen to be the $z$-​di­rec­tion. In par­tic­u­lar, for fermi­ons with spin $\leavevmode \kern.03em\raise.7ex\hbox{\the\scriptfont0 1}\kern-.2em /\kern-.21em\lower.56ex\hbox{\the\scriptfont0 2}\kern.05em$, in­clud­ing elec­trons, there is a spin-up” and a “spin-down ver­sion of each spa­tial en­ergy eigen­func­tion:

$$\begin{eqnarray*} \pp{n_xn_yn_z,\frac12}/{\skew0\vec r}//z/ & = & \sqrt{\frac{... ...\cal V}}}\; \sin(k_xx) \sin(k_yy) \sin(k_zz) \;{\downarrow}(S_z) \end{eqnarray*}$$

That means that each point in the wave num­ber space fig­ure 6.1 stands for two sin­gle-par­ti­cle states, not just one.

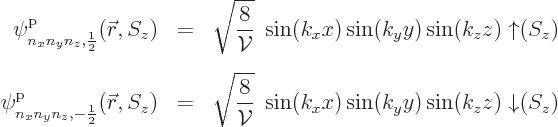
In gen­eral, if the par­ti­cles have spin $s$, each point in wave num­ber space cor­re­sponds to $2s+1$ dif­fer­ent sin­gle-par­ti­cle states. How­ever, pho­tons are an ex­cep­tion to this rule. Pho­tons have spin $s$ $\vphantom0\raisebox{1.5pt}{$=$}$ 1 but each spa­tial state cor­re­sponds to only 2 sin­gle-par­ti­cle states, not 3. (That is re­lated to the fact that the spin an­gu­lar mo­men­tum of a pho­ton in the di­rec­tion of mo­tion can only be $\hbar$ or $\vphantom{0}\raisebox{1.5pt}{$-$}$$\hbar$, not 0. And that is in turn re­lated to the fact that the elec­tro­mag­netic field can­not have a com­po­nent in the di­rec­tion of mo­tion. If you are cu­ri­ous, see ad­den­dum {A.21.6} for more.)

Key Points

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

Each sin­gle par­ti­cle state is char­ac­ter­ized by a set of three wave num­bers $k_x$, $k_y$, and $k_z$.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

Each point in the wave num­ber space fig­ure 6.1 cor­re­sponds to one spe­cific spa­tial sin­gle-par­ti­cle state.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

The dis­tance of the point from the ori­gin is a mea­sure of the en­ergy of the sin­gle-par­ti­cle state.

$\begin{picture}(15,5.5)(0,-3) \put(2,0){\makebox(0,0){\scriptsize\bf0}} \put(12... ...\thicklines \put(3,0){\line(1,0){12}}\put(11.5,-2){\line(1,0){3}} \end{picture}$

In the pres­ence of nonzero par­ti­cle spin $s$, each point in wave num­ber space cor­re­sponds to $2s+1$ sep­a­rate sin­gle-par­ti­cle states that dif­fer in the spin in the cho­sen $z$-​di­rec­tion. For pho­tons, make that $2s$ in­stead of $2s+1$.