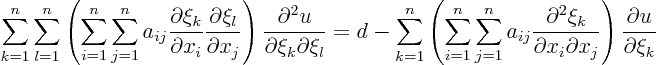| Partial Differential Equations 0.15 alpha |
|
© Leon van Dommelen |
|
D.3 Coordinate transformation derivation
This note derives the coordinate transformation formulae
of chapter 1.4.2.
According to the total differential formula from calculus:
This formula is used to transform the first order derivatives of 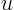 .
.
Differentiating once more, using the product rule of differentiation
and again the total differential formulae for the first factor of the
product:
If you plug the formula for the second order derivatives above into
the left hand side of the original partial differential equation and
rearrange, you get the transformed equation.
The coefficients of the transformed matrix 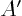 and the transformed
right hand side can be read off from the above expression.
and the transformed
right hand side can be read off from the above expression.
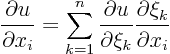
![\begin{displaymath}
\frac{\partial^2 u}{\partial x_i\partial x_j} =
\sum_{k=...
...
\frac{\partial^2 \xi_k}{\partial x_i\partial x_j}
\right]
\end{displaymath}](img1547.gif)