|
|
|
|
|
Next: 3.2 Numerical solution |
|
The general quasi-linear first order equation in two dimensions takes
the form
The characteristics are defined by
In general, the variation of a function ![]() of two variables along
a line is given by the total differential of calculus,
of two variables along
a line is given by the total differential of calculus,
Note that frequently, you may have to solve the ordinary differential equations in a different
form or order. For example, if ![]() depends on
depends on ![]() , you will not be
able to solve
, you will not be
able to solve
![]() to find
to find ![]() as a function of
as a function of ![]() since
since
![]() in
in ![]() is still an unknown function of
is still an unknown function of ![]() . But maybe, say,
. But maybe, say,
![]() is not a function of
is not a function of ![]() , in which case you could solve
, in which case you could solve
![]() ; then you could plug that solution for
; then you could plug that solution for ![]() as a
function of
as a
function of ![]() into
into
![]() to get an equation for
to get an equation for ![]() that
no longer involves
that
no longer involves ![]() . The bottom line is that it is really best
to write the characteristic equations as
. The bottom line is that it is really best
to write the characteristic equations as
In all the unsolved problems in the book, there is at least one solvable ratio. But if there is none, you may be forced to try to change variables, e.g. to polar, or eliminate one variable by, say, differentiating a ratio, hopefully producing a second order ordinary differential equation with one variable eliminated.
ExampleQuestion: (5.30) Solve
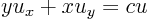
Solution:
This example wants to solve the partial differential equation
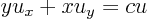
For this equation, a ratio likeis not immediately solvable for
, since
besides
would be an unknown function of
. The only solvable ratio is in fact that between
and
:
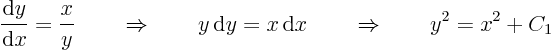
whereis the integration constant. These characteristic lines are hyperbola; they are sketched in figure 3.1.
Now that
is a known function of
, specifically
assuming it is positive, the ordinary differential equation for
can be solved
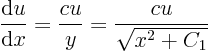
to give
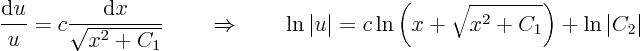
Taking exponentials and noting that the square root equals, this simplifies to
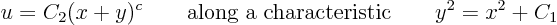
For example, if it is given that
at the point
shown as a fat dot in figure 3.2, then it follows from the above general expressions that
, so the characteristic line is the line
shown in grey, and that
, so you would get
for
on the grey line.
Figure 3.2: Given the value of at a single point on a characteristic line,
can be found at every point on that line.
ExampleQuestion: (5.6) Solve the nasty example
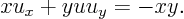
Solution:
In this case, none of the ratios
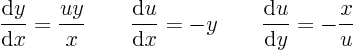
is a solvable ordinary differential equation; each involves three variables. You might try to take a derivative of an equation, like
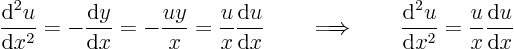
which is indeed an ordinary differential equation fornot involving the unknown
. But it is an awkward second order nonlinear equation.
The trick is to guess that the combination
can be found as a function of
:
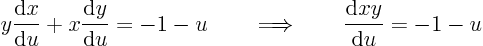
which produces
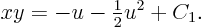
This can then be plugged into
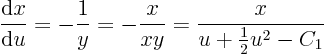
to get a separable equation givingas a function of
, with another integration constant
. However, that becomes a mess, involving either an arctan or logarithm, depending on the value of
.