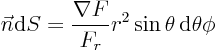|
|
|
|
Skip to: 2.3.7 The integral formula for the Neumann problem |
|
Derive the Poisson integral formula in three dimensions as given in the previous subsection.
Answer:
In two dimensions the source distribution drops out completely. In three dimensions, both the source and dipole distributions stay.
In particular, you cannot get
![]() to be zero. You can however take
to be zero. You can however take ![]() so that it only involves the given
so that it only involves the given ![]() on the boundary, not the unknown radial derivative of
on the boundary, not the unknown radial derivative of ![]() .
.
Then you will need to combine

If you cannot find the unit vector
![]() in spherical coordinates, evaluate it as
in spherical coordinates, evaluate it as ![]() with
with
![]() expressed in spherical coordinates. Use trig to clean up the dot product
expressed in spherical coordinates. Use trig to clean up the dot product
![]() a bit.
a bit.
Also, in an earlier homework you, hopefully, showed that in spherical coordinates