|
|
|
To: 7.2.4 Summary |
The drift velocity of two counter-rotating point vortices in
an inviscid
(to be precise, for ![]() and
and ![]() finite) fluid is simple:
the vortex pair drifts in the direction of the
symmetry line (here the
finite) fluid is simple:
the vortex pair drifts in the direction of the
symmetry line (here the ![]() -axis) at constant speed
[230].
Further, in the inviscid case the positions of the vortices are simple
to identify since the
point vortices remain point vortices
-axis) at constant speed
[230].
Further, in the inviscid case the positions of the vortices are simple
to identify since the
point vortices remain point vortices
However, in a viscous fluid the vortex pair diffuses, and changes shape
and speed as it drifts.
Hence, before we can compare the numerical results, we need to define
first what point will be taken as the ``position" of the vortex pair.
Different authors have used different points to measure the
position; the time derivatives
of these different points imply different drift velocities.
We will first review some of these definitions.
Since the flow is symmetric about the ![]() -axis,
we will focus on the flow in one half plane bounded by this
symmetry line.
One way to define a position of the vortex in the chosen half plane is
to average over the vorticity:
-axis,
we will focus on the flow in one half plane bounded by this
symmetry line.
One way to define a position of the vortex in the chosen half plane is
to average over the vorticity:
The limiting behaviors of the drift velocities defined above
are investigated by Van Dommelen & Shankar
[230] for small times, for small Reynolds
numbers, and for large times using asymptotic expansions.
In the following paragraphs, we compare the numerical results
obtained using the vorticity redistribution method
with the analytical solutions obtained there.
The Reynolds number in the computation ranges from
0 to 100 based on the initial drift velocity.
The computational results presented in this subsection were obtained
at a diffusion time step
![]() and were repeated at
and were repeated at ![]() to verify their accuracy. At the highest Reynolds number
to verify their accuracy. At the highest Reynolds number ![]() ,
we halved the time step again (to 0.001) to eliminate some unsightly,
but inconsequential wiggles.
In addition, for shorter times, computations were conducted at a
still smaller time step (
,
we halved the time step again (to 0.001) to eliminate some unsightly,
but inconsequential wiggles.
In addition, for shorter times, computations were conducted at a
still smaller time step (
![]() )
to verify very small perturbations
in the small time analytical solution.
)
to verify very small perturbations
in the small time analytical solution.
Figure 7.12 shows analytical and semi-analytical results of
Van Dommelen & Shankar [230] for
the computed velocities ![]() ,
, ![]() and
and ![]() for Reynolds number
for Reynolds number ![]() ,
as well as the small and large time expansions for that case.
At small times, the average velocity
,
as well as the small and large time expansions for that case.
At small times, the average velocity ![]() and the
vortex center velocity
and the
vortex center velocity ![]() remain
exponentially close to
the unit inviscid drift velocity.
On the other hand, the velocity
remain
exponentially close to
the unit inviscid drift velocity.
On the other hand, the velocity ![]() decreases proportional to the diffusion time
decreases proportional to the diffusion time ![]() .
Figure 7.12 also shows that the asymptotic values
for the average velocity
.
Figure 7.12 also shows that the asymptotic values
for the average velocity ![]() and velocity
and velocity ![]() for large times
are still quite inaccurate at the maximum times
presented here.
The computed vortex center velocity
for large times
are still quite inaccurate at the maximum times
presented here.
The computed vortex center velocity ![]() tends to the
computed velocity
tends to the
computed velocity ![]() for large times; but the
computed average velocity
for large times; but the
computed average velocity ![]() remains
larger than these two velocities by about
remains
larger than these two velocities by about ![]() [230].
[230].
As shown
in figures 7.13 and 7.14,
our computed results at a very fine
time step (
![]() ) correctly follow the analytical
predictions for small times [230].
Note that this indicates
excellent performance of the numerical method: the graph verifies very
small deviations from the inviscid drift velocity.
Furthermore, the velocity is almost singular at those times.
In figures 7.13 and 7.14,
the exact Stokes solution for
) correctly follow the analytical
predictions for small times [230].
Note that this indicates
excellent performance of the numerical method: the graph verifies very
small deviations from the inviscid drift velocity.
Furthermore, the velocity is almost singular at those times.
In figures 7.13 and 7.14,
the exact Stokes solution for ![]() , has also been shown.
At larger times all computed curves should approach the Stokes curve
since the decay of the circulations of the vortices
reduces the effects of convection. This is consistent with our numerical
results.
, has also been shown.
At larger times all computed curves should approach the Stokes curve
since the decay of the circulations of the vortices
reduces the effects of convection. This is consistent with our numerical
results.
 |
 |
 |
 |
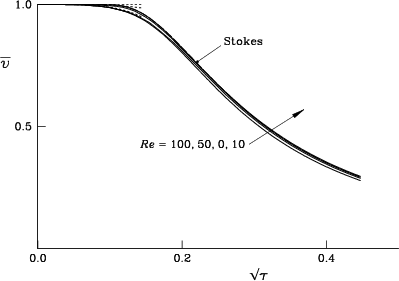
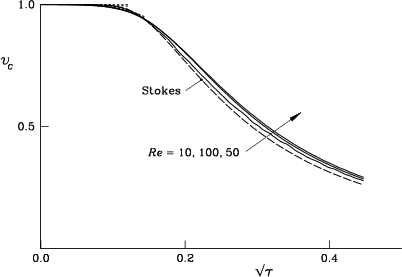
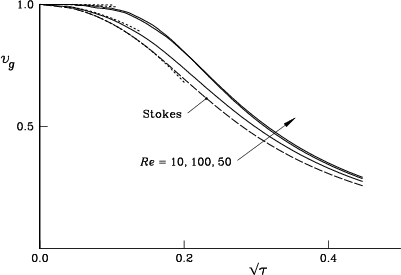
Figures 7.15, 7.16, and 7.17
show the computed average velocity ![]() , vortex center velocity
, vortex center velocity
![]() and the velocity
and the velocity ![]() for Reynolds numbers 10, 50, and 100.
No dramatic changes from Stokes flow
are observed for the studied Reynolds numbers.
Moreover, the different computed velocities have an interesting tendency
to approach each other when the Reynolds number increases.
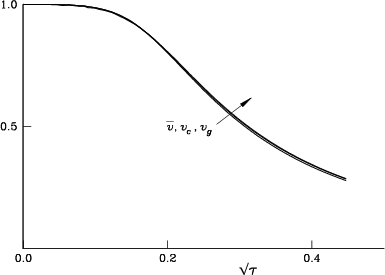
For example, figure 7.18 compares these velocities
at Reynolds number 100.
Theoretical reasons why this would be so can be found in
Van Dommelen & Shankar [230].
for Reynolds numbers 10, 50, and 100.
No dramatic changes from Stokes flow
are observed for the studied Reynolds numbers.
Moreover, the different computed velocities have an interesting tendency
to approach each other when the Reynolds number increases.
For example, figure 7.18 compares these velocities
at Reynolds number 100.
Theoretical reasons why this would be so can be found in
Van Dommelen & Shankar [230].