EGN 5456 Computational Mechanics 10/27/97
Open book Van Dommelen 1:05-2:20pm

Show all reasoning and intermediate results leading to your answer.

1.

Consider steady heat conduction in a plate with the elliptical boundary x² + y²/4 = 1. The temperature on the elliptical boundary is T=x. Draw the isotherms $T=0, \pm 0.25, \pm 0.5, \pm 0.75$ inside the plate. Now assume that we increase the boundary temperature on the right side of the boundary, to T=1+x, and reduce it on the left side of the boundary, to T=-1+x. Sketch the isotherms $T= 0, \pm 0.5, \pm 1, \pm 1.5$inside the plate.

2.

Consider entropy convection inside a pipe bend into a closed ring of unit radius. The nonconducting inviscid entropy equation is s_t + u s_x = 0. Assume u is a constant velocity. Show that a solution to this problem is

$$s = \sum_{k=-\infty}^\infty C_k e^{ikx} e^{-ikut},$$

where $i=\sqrt{-1}$. What determines the constants C_k? Why is this form of solution with complex exponentials e^ikx more convenient than the real form

$$s = \sum_{k=-\infty}^\infty A_k(t) \cos(kx) + B_k(t) \sin(kx),$$

aside from the fact that there are now two different types of terms?

3.

The one-dimensional inviscid momentum equation for flow in a pipe is

$$(\rho u)_t + (\rho u^2)_x + p_x = 0.$$

From this equation, derive a conservation law for an arbitrary piece of pipe with moving end points. From it, show that you can get the momentum equation in the way expressed in your physics classes.

4.

Consider one-dimensional inviscid nonconducting isentropic flow in a pipe. The governing equations can be expressed in terms of the flow velocity $\bar u$,the speed of sound $\bar a$, and the ratio of specific heats $\gamma=1.4$ as:

$$\begin{array} {rcl} \bar a_t + \bar u \bar a_x + \frac{\gam... ...bar u_x + \frac2{\gamma-1} \bar a \bar a_x & = & 0 \end{array}$$

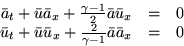
To simplify, we will linearize this to

$$\begin{array} {rcl} {a}_t + u_0 {a}_x + \frac{\gamma-1}2 a_... ...t + u_0 {u}_x + \frac2{\gamma-1} a_0 {a}_x & = & 0 \end{array}$$

where u₀ and a₀ are now constant reference values of the velocity and speed of sound, and u and a are the perturbation velocity and speed of sound to be found. Classify this system of equations for u and a. Find the Riemannian invariants and solve if the initial velocity $u(x,0)=\sin(x)$ and the speed of sound a(x,0)=0.