| Spring 2007 Homework Problems |
|
© Leon van Dommelen |
Analysis II Spring 2007
Homework Problems
Do not print out this page. Keep checking for changes. Complete assignment
will normally be available the day after the last lecture whose material
is included in the test (Saturday, normally).
- 01/17 W
-
- p13, q31
- p13, q32
- p14, q48
- p32, q66
- p32, q69
- p32, q87
- p53, q32
- 01/24 W
-
- p54, q47
- p78, q54
- p78, q62
- p78, q64
- p79, q70
- p79, q72
- p80, q96
- 02/31 W
-
- p78, q46
- p78, q60
- p80, q84
- p80, q102
- p102, q32
- p103, q44
- 02/07 W
-
- p104, q63
- p104, q62 (use Cartesian coordinates except in the actual integration)
- p132, q39 (use Cartesian coordinates except in the actual integration)
- p132, q42
- p132, q44
- p133, q56
- p160, q37
- p160, q38
- 02/14 W
-
- p160, q43
- p160, q44
- p160, q47 (finish)
- Find the scale factors
 and
and  of polar coordinates
in two dimensions.
of polar coordinates
in two dimensions.
- Use them to find the Laplacian in polar coordinates.
- The PDE problem
 in the first quadrant,
with boundary conditions
in the first quadrant,
with boundary conditions  ,
,  has two possible
solutions:
has two possible
solutions:
 for
for  and
and  for
for  in Cartesian coordinates.
in Cartesian coordinates.
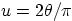 in polar coordinates.
in polar coordinates.
Show that both solutions satisfy the PDE and boundary conditions.
So, which solution is correct, and why?
- Consider the following steady heat conduction problem for a
triangular plate of a material with unit heat conduction
coefficient
 :
:
- the temperature is zero on the side
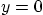 of the plate;
of the plate;
- the heat flux coming out of the side
 of the plate is
zero;
of the plate is
zero;
- the heat flux entering the third side
 is constant
and equal to one.
is constant
and equal to one.
Write the partial differential equation and all three boundary
conditions as mathematical equations for the temperature  .
.
- Which of the following possibilities is the correct temperature
distribution for the previous problem: (a)
 ;
(b)
;
(b)  ;
(c)
;
(c)  ?
Explain why.
?
Explain why.
- If steady heat conduction satisfies
 ,
what does the divergence theorem tell us about Neumann boundary
conditions? Explain this physically. Does the same apply to
the unsteady heat equation?
,
what does the divergence theorem tell us about Neumann boundary
conditions? Explain this physically. Does the same apply to
the unsteady heat equation?
- Which of the following situations is described by the
inhomogeneous Laplace equation (the Poisson equation):
- the membrane of a drum when it is being played;
- the membrane of a drum when the drum sticks and various
other stuff are resting on top of it;
- the membrane of a drum when you drop it.
Explain why.
- 02/23 F
-
- Show that the following solution satisfies both the heat
equation
 and the wave equation
and the wave equation  for
for  and
and  :
:
It is a valid solution to only one equation, however. Which one,
and why?
- Show that the following solution satisfies both the heat
equation
 and the wave equation
and the wave equation  for
for  and
and  :
:
It is a valid solution to neither equation, however. Why not?
- Write the physical problem of heat conduction in a iron bar
(iron heat conduction coefficient
 W/m-K, density
W/m-K, density
 kg/m
kg/m , specific heat
, specific heat  kJ/kg-K)
of length 2 m and diameter 10 cm in terms of the temperature
kJ/kg-K)
of length 2 m and diameter 10 cm in terms of the temperature  if one end is at 25
if one end is at 25 C and 20 W of heat is entering the bar at
the other end. Also, at time zero the bar is at a uniform
25
C and 20 W of heat is entering the bar at
the other end. Also, at time zero the bar is at a uniform
25 C throughout. List PDE, BCs, and IC in the
C throughout. List PDE, BCs, and IC in the  -plane
with all numerical constants filled in, but do not try to solve.
We will learn how to solve later, Hint: use units!
-plane
with all numerical constants filled in, but do not try to solve.
We will learn how to solve later, Hint: use units!
- For acoustics in a pipe, the (small) axial air velocity
 satisfies Newton's second law
satisfies Newton's second law
where  is the mass per unit volume, which can be approximated
as constant and equal to 1.225 kg/m
is the mass per unit volume, which can be approximated
as constant and equal to 1.225 kg/m and
and  is the pressure
in Pa. The pressure variations are caused by motion-induced
fluid compression according to the “continuity equation”
is the pressure
in Pa. The pressure variations are caused by motion-induced
fluid compression according to the “continuity equation”
where  is the speed of sound, 340 m/s. Reduce these two
equation to a wave equation for the pressure
is the speed of sound, 340 m/s. Reduce these two
equation to a wave equation for the pressure  . Then write
the problem for the gage pressure in a pipe of length 0.5 m if
one end of the pipe is closed (zero fluid velocity at that end)
and the other end of the pipe is open. Assume the initial
pressure in the pipe is uniform at 5 Pa gage, and the air velocity
is zero, but then at time
zero we take our thumb of the open end and from then on the
pressure at the open end is ambient at zero gage. List PDE, BCs,
and IC in the
. Then write
the problem for the gage pressure in a pipe of length 0.5 m if
one end of the pipe is closed (zero fluid velocity at that end)
and the other end of the pipe is open. Assume the initial
pressure in the pipe is uniform at 5 Pa gage, and the air velocity
is zero, but then at time
zero we take our thumb of the open end and from then on the
pressure at the open end is ambient at zero gage. List PDE, BCs,
and IC in the  -plane with all numerical constants filled in,
but do not try to solve. We will learn how to solve later, Hint:
use units!
-plane with all numerical constants filled in,
but do not try to solve. We will learn how to solve later, Hint:
use units!
- Identify the wave propagation speed
 in a string under
a tension force of 30 N with a mass per unit length of 0.002 kg/m.
Hint; use units!
in a string under
a tension force of 30 N with a mass per unit length of 0.002 kg/m.
Hint; use units!
- Solve the one-way wave equation in the infinite domain
 if the initial entropy
if the initial entropy  is
a given function
is
a given function  . Note that the flow velocity
. Note that the flow velocity  simply translates the entropy distribution along the
simply translates the entropy distribution along the  -axis.
-axis.
- 2.19(b)
- 02/28 W
-
- 2.19(d)
- 2.19(h)
- 2.20
- 2.21 (a) and (b) in 3 spatial dimensions
- 03/14 W
-
- Use the 2D PDE transformation formulae derived in class to
transform the Laplace equation
 to polar
coordinates and see whether you get the correct result.
to polar
coordinates and see whether you get the correct result.
- 2.24
- 2.25
- Get rid of the first order derivatives in the problem 2.25 by
defining a new unknown
 where
where
 are the rescaled coordinates and
are the rescaled coordinates and  ,
,
 , and
, and  are constants to be found.
are constants to be found.
- 03/21 W
-
- 2.22 b, g (sketch the characteristics)
- 2.27 a, b
- 2.28 d (solve the PDE)
- 2.28 f (solve the PDE)
- 2.28 c (solve the PDE)
- 2.28 k
- 2.28 b Check that indeed
 and
and  and find
and find  . We
learned previously that constant coefficient elliptic problems can
be reduced to the Laplacian by rotating the coordinates to
. We
learned previously that constant coefficient elliptic problems can
be reduced to the Laplacian by rotating the coordinates to
 , and then stretching these to orthogonal coordinates
, and then stretching these to orthogonal coordinates
 . But the coordinates
. But the coordinates  and
and  are not
orthogonal (the lines of constant
are not
orthogonal (the lines of constant  and
and  are under an
oblique angle.) Should not the transformation that reduces the
PDE to the Laplace equation be unique??
are under an
oblique angle.) Should not the transformation that reduces the
PDE to the Laplace equation be unique??
- Show that one of the below Laplace equation problems has a
unique solution,
 , but the other has multiple solutions:
, but the other has multiple solutions:
Hint: to show uniqueness, use the notes. To show nonuniqueness
of the other problem, guess a simple nonzero solution.
- Solve the heat conduction problem in infinite two-dimensional space
 ,
,
 if heat is being added to the
point at the origin at a unit rate.
if heat is being added to the
point at the origin at a unit rate.
- Find the Green's function of the Poisson equation in infinite
two-dimensional space. Comment on its behavior at large distances
compared to the three-dimensional Green's function.
- Solve the Poisson equation in infinite two-dimensional space.
Rigor is not required.
- 03/23 F
-
- Consider the Poisson or Laplace problem in a two-dimensional
finite region
 :
:
with  and
and  given constants and
given constants and  and
and  given functions
(and
given functions
(and  in the Laplace case.)
in the Laplace case.)
Suppose we define  outside the region
outside the region  to be a chosen
function
to be a chosen
function  that satisfies the Laplace equation, like
for example
that satisfies the Laplace equation, like
for example  . Explain why the thus defined
. Explain why the thus defined
 in all of space is not the infinite space solution
in all of space is not the infinite space solution
that you derived for the infinite space problem. After all,
 has the same Laplacian everywhere:
has the same Laplacian everywhere:
 inside
inside  and
and
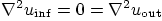 outside
outside  . Should not solutions to
the infinite space Poisson equation be unique?
. Should not solutions to
the infinite space Poisson equation be unique?
The integral
is not quite proper. For one, G is infinite at the point
 so we would be integrating infinity. Also,
integrals must be done over finite regions, not infinite ones.
Define
so we would be integrating infinity. Also,
integrals must be done over finite regions, not infinite ones.
Define
 more carefully to avoid these problems
by using limits of integrals, sketching the region of integration.
more carefully to avoid these problems
by using limits of integrals, sketching the region of integration.
- Work out the more careful expression for
 to
get a relation showing the difference between
to
get a relation showing the difference between  and
and
 . Hint: use Green's second identity. You may assume
that at a large distance
. Hint: use Green's second identity. You may assume
that at a large distance  from the point
from the point  ,
,
 can be approximated as
can be approximated as  where
where  and
and  are
constants.
are
constants.
- Except for the constant, graphically explain the physical
meaning of the effect of the boundary conditions, i.e. explain the
difference between
 and
and  in physical terms.
in physical terms.
- 03/28 W
-
- Show that if
 satisfies the Laplace equation
satisfies the Laplace equation
 inside the unit circle around the origin, then
inside the unit circle around the origin, then
 satisfies the Laplace
equation outside the unit circle. Hint: write
satisfies the Laplace
equation outside the unit circle. Hint: write
 where
where  then
work out
then
work out
 in terms of the
in terms of the  derivatives
of
derivatives
of
 and show it is a multiple of the Laplacian of
and show it is a multiple of the Laplacian of
 .
.
- For the Dirichlet problem for the Laplace equation in a unit
circle,
choose  in Green's integral expression for
in Green's integral expression for  so that
the unknown boundary heat flux disappears.
so that
the unknown boundary heat flux disappears.
- To get rid of the constant
 , show that it is equal to
, show that it is equal to
by using the mean value theorem 3.1, proved in problem 3.1.
- Show that Green's formula then reduces to the two-dimensional
case of (3.5) in the book.
- Work out the integral to obtain the familiar form of Poisson's
integral formula in two dimensions, given in problem 3.37.
- 04/04 W
-
- 3.38 Think of it as a problem with negative temperatures at one
side of the circle and positive at the other side. The temperature at
the center is asked.
- 3.39 Hint: the solution inside the circle is easy to guess.
- 3.41 Remember Gauss.
- 4.20 A number
 is rational if it can be written as the ratio of
a pair of integers, eg 1.5 = 3/2 = 6/4 = 9/6 = ...
It is irrational if it cannot, like
is rational if it can be written as the ratio of
a pair of integers, eg 1.5 = 3/2 = 6/4 = 9/6 = ...
It is irrational if it cannot, like  . Near any
rational number, irrational numbers can be found infinitely closely
nearby, and vice versa. For nonzero solutions, try
. Near any
rational number, irrational numbers can be found infinitely closely
nearby, and vice versa. For nonzero solutions, try
 , which satisfies the wave equation
and the boundary conditions at
, which satisfies the wave equation
and the boundary conditions at  and
and  and the
initial condition at
and the
initial condition at  . See when it satisfies the end
condition at
. See when it satisfies the end
condition at  .
.
This is the boundary value problem for the wave equation, and would
be perfectly OK for if it would have been the Laplace equation.
(For the Laplace equation, the  becomes
becomes
 and only a unique, zero, solution is possible.)
The wave equation needs two initial conditions at
and only a unique, zero, solution is possible.)
The wave equation needs two initial conditions at  , not one
condition at
, not one
condition at  and one at
and one at  .
.
- Suppose the initial conditions to the wave equation
 in infinite space
in infinite space
 are
nonzero only from
are
nonzero only from 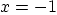 to
to  . Identify the regions in the
. Identify the regions in the
 -plane where
-plane where  will be zero and where it will in general be
nonzero.
will be zero and where it will in general be
nonzero.
- Plot the solution to the wave equation in an infinite acoustic pipe,
if the initial conditions are
where  for all
for all  while
while  for
for  and
and  everywhere else. In particular, plot
everywhere else. In particular, plot  versus
versus  at times
at times
 ,
,  ,
,  ,
,  ,
,  , and
, and  .
.
Hint: First plot the anti-derivative of  , call it
, call it  ,
against
,
against  . The integration constant is not important, you can
take
. The integration constant is not important, you can
take
 . For example,
. For example,  will be one then. Write the D'Alembert solution in terms of
function
will be one then. Write the D'Alembert solution in terms of
function  , then graphically evaluate and sum the relevant
parts.
, then graphically evaluate and sum the relevant
parts.
- 5.25
- 5.27 (b)
- Refer to problem 5.34. Find the general solution to
 using the method of characteristics. Write down both
possible forms in which the solution can be written.
(
using the method of characteristics. Write down both
possible forms in which the solution can be written.
( or
or  .)
.)
- Verify that both of the solutions
 and
and  given in 5.34
are in each region of at least one of the two forms and identify
what the arbitrary function in the general solution is then.
given in 5.34
are in each region of at least one of the two forms and identify
what the arbitrary function in the general solution is then.
- Neatly draw the characteristic lines of each of the solutions
 and
and  as well as the shocks at
as well as the shocks at  and
and  of
of  ,
and the single shock at
,
and the single shock at  of
of  . Put several
characteristics in each region (including in
. Put several
characteristics in each region (including in  for
for  and
and  for
for  .) Draw up to
.) Draw up to  , say.
, say.
- Convert the PDE
 to a conservation form
to a conservation form
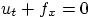 and thus determine what functions
and thus determine what functions  is. What is
the conserved integral?
is. What is
the conserved integral?
- Verify that all three shocks satisfy the shock conservation
law
 assuming
assuming  . Here 1 is the point
immediately to the left of the shock and 2 the point immediately
to the right of it, and
. Here 1 is the point
immediately to the left of the shock and 2 the point immediately
to the right of it, and  is the shock velocity.
is the shock velocity.
- Show that one of the three shocks does not satisfy the
“entropy condition”
 . Such a shock
represents an unphysical “expansion shock,” and the
corresponding solution must be rejected. For physical solutions
the velocity
. Such a shock
represents an unphysical “expansion shock,” and the
corresponding solution must be rejected. For physical solutions
the velocity  of the characteristics before the shock must
be greater than the shock velocity
of the characteristics before the shock must
be greater than the shock velocity  for the characteristics
to catch up with the shock. The shock velocity
for the characteristics
to catch up with the shock. The shock velocity  must be
greater than the velocity
must be
greater than the velocity  of the characteristics behind the
shock for the shock to be able to catch up with those
characteristics.
of the characteristics behind the
shock for the shock to be able to catch up with those
characteristics.
- 04/11 W
-
- Solve 7.27 using D'Alembert, graphically identifying all
functions involved in terms of the given
 and
and  .
.
- Using the solution of the previous problem, and taking
 ,
,  ,
,  , and
, and  , draw
, draw  as a
function of
as a
function of  . Note that the boundary conditions are now
satisfied, though the initial condition did not.
. Note that the boundary conditions are now
satisfied, though the initial condition did not.
- Using the solution of the previous problems, find
 .
.
- Find the separation of variables eigenfunctions of 7.27. Make
very sure you do not miss one.
- Write the solution to
 in terms of the derived
eigenfunctions and plug into the PDE to find expressions for the
coefficients. Be very careful to solve special cases separately
to get them right.
in terms of the derived
eigenfunctions and plug into the PDE to find expressions for the
coefficients. Be very careful to solve special cases separately
to get them right.
- Find the undetermined coefficients in the solution for
 by
setting
by
setting  and
and  equal to the given functions
equal to the given functions
 and
and  . Assume again that
. Assume again that  ,
,  and
and
 . Hint: the coefficients corresponding to
. Hint: the coefficients corresponding to  can
easily be guessed.
can
easily be guessed.
- Make a computer plot of
 versus
versus  at times
at times  ,
,
 ,
,  ,
,  ,
,  , and
, and  . Use whatever
software you like. Note: the error is of order
. Use whatever
software you like. Note: the error is of order  , if
, if  is
the eigenfunction number, so you want to sum at least about 15
terms for one percent error. Compare the solution at
is
the eigenfunction number, so you want to sum at least about 15
terms for one percent error. Compare the solution at  with
the one you got from D'Alembert, and the solution at
with
the one you got from D'Alembert, and the solution at  with
the given initial condition. Since
with
the given initial condition. Since  initially, you would
expect
initially, you would
expect
 . Is it?
. Is it?
- Replot summing only one, two, and three eigenfunctions and
examine how the solution approaches the exact one if you sum more
and more terms. Comment in particularly on the slope of the
profiles at time
 and
and  at the boundaries. What should
the slope be at those times? What is it?
at the boundaries. What should
the slope be at those times? What is it?
- 04/18 W
-
- Refer to problem 7.19. Find a function
 that satisfies
the inhomogeneous boundary conditions.
that satisfies
the inhomogeneous boundary conditions.
- Continuing the previous problem, define
 . Find
the PDE, BC and IC satisfied by
. Find
the PDE, BC and IC satisfied by  .
.
- Find eigenfunctions in terms of which
 may be written, and
that satisfy the homogeneous boundary conditions.
may be written, and
that satisfy the homogeneous boundary conditions.
- Solve for
 using separation of variables in terms of
expressions in terms of the known functions
using separation of variables in terms of
expressions in terms of the known functions  ,
,  , and
, and
 .
.
- 7.26. Note: you can simplify the problem to a standard heat
conduction one by defining
 for
suitable constants
for
suitable constants  and
and  . Alternatively, you can
just solve it directly. Either way, the answer in the book is
wrong.
. Alternatively, you can
just solve it directly. Either way, the answer in the book is
wrong.
- 7.35. Minor error in the book's answer.
![]() outside the region
outside the region ![]() to be a chosen
function
to be a chosen
function ![]() that satisfies the Laplace equation, like
for example
that satisfies the Laplace equation, like
for example ![]() . Explain why the thus defined
. Explain why the thus defined
![]() in all of space is not the infinite space solution
in all of space is not the infinite space solution
![]() becomes
becomes
![]() and only a unique, zero, solution is possible.)
The wave equation needs two initial conditions at
and only a unique, zero, solution is possible.)
The wave equation needs two initial conditions at ![]() , not one
condition at
, not one
condition at ![]() and one at
and one at ![]() .
.
![]() , call it
, call it ![]() ,
against
,
against ![]() . The integration constant is not important, you can
take
. The integration constant is not important, you can
take
![]() . For example,
. For example, ![]() will be one then. Write the D'Alembert solution in terms of
function
will be one then. Write the D'Alembert solution in terms of
function ![]() , then graphically evaluate and sum the relevant
parts.
, then graphically evaluate and sum the relevant
parts.