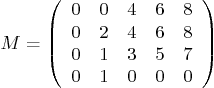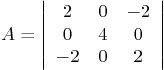EML 5060 Analysis in Mechanical Engineering 11/09/18
Closed book Van Dommelen 12:30-1:20 pm
Solutions should be fully derived showing all intermediate
results, using class procedures. Show all reasoning. Bare
answers are absolutely not acceptable, because I will assume they come
from your calculator (or the math handbook, sometimes,) instead of
from you. You must state what result answers what part of the
question. Answer what is asked; you do not get any credit for making
up your own questions and answering those. Use the stated procedures.
Give exact, fully simplified, answers where possible.
You must use the systematic procedures described in class, not
mess around randomly until you get some answer. Echelon form is
defined as in the lecture notes, not as in the book. Eigenvalues must
be found using minors only. Eigenvectors must be found by identifying
the basis vectors of the appropriate null space. Eigenvectors of
symmetric matrices must be orthonormal. If there is a quick way to do
something, you must use it.
One book of mathematical tables, such as Schaum's Mathematical
Handbook, may be used, as well as a calculator, and a handwritten
letter-size formula sheet.
- Background: Finding the possible internal stress fields in
structures requires finding the null space of the matrix of the
governing equilibrium equations.
Question: For the matrix
(a) Find the null space. (b) Find a basis for the null space. (c)
Find the dimension of the null space. (d) Find the dimension of the
row space, the dimension of the column space, and the rank. Explain
how you got those values. (Always identify what answers what.)
Solution.
- Background: For purposes such as analyzing natural
frequencies, sometimes an analytical expression of a determinant is
needed.
Question: Find, without any row (or column) operations
At every stage, choose the approach that requires the smallest
possible number of terms. If you do it correctly, it will be quick.
Solution.
- Background: Matrix diagonalization is one of the most
important tricks in physics and engineering, from analyzing stress
fields, solid body dynamics, to finding quantized quantities.
Question: Using class procedures, find the transformation
matrix that reduces the matrix
to diagonal form. Note: put the eigenvalues in order from smallest
to largest. Neatly draw the original 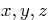 coordinate system,
with the
coordinate system,
with the 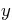 -axis going away from you and
-axis going away from you and 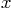 to the right. In that
drawing, show the labeled new
to the right. In that
drawing, show the labeled new 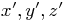 axis system in which the
matrix is diagonal, and indicate the value of the appropriate
rotation angle(s). Finally, give the “transformation matrix
from new to old,” and the expressions for
axis system in which the
matrix is diagonal, and indicate the value of the appropriate
rotation angle(s). Finally, give the “transformation matrix
from new to old,” and the expressions for 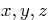 in terms of
in terms of
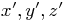 and vice-versa.
and vice-versa.
Solution.