EML 5060 Analysis in Mechanical Engineering 11/06/15
Closed book Van Dommelen 12:30-1:20 pm
Solutions should be fully derived showing all intermediate
results, using class procedures. Show all reasoning. Bare
answers are absolutely not acceptable, because I will assume they come
from your calculator (or the math handbook, sometimes,) instead of
from you. You must state what result answers what part of the
question. Answer exactly what is asked; you do not get any credit for
making up your own questions and answering those. Use the stated
procedures. Give exact, fully simplified, answers.
You must use the systematic procedures described in class, not
mess around randomly until you get some answer. Echelon form is
defined as in the lecture notes, not as in the book. Eigenvalues must
be found using minors only. Eigenvectors must be found by identifying
the basis vectors of the appropriate null space. Eigenvectors to
symmetric matrices must be orthonormal. If there is a quick way to do
something, you must do it.
One book of mathematical tables, such as Schaum's Mathematical
Handbook, may be used, as well as a calculator, and a handwritten
letter-size formula sheet.
- Background: Vector analysis is often the most easy,
systematic, and reliable way to figure out geometric problems.
Question: Given the position vectors from the origin 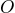 :
:
Find
- the area of the parallelogram with sides
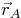 and
and
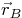 ;
;
- the area of the triangle with sides
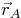 and
and
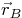 ;
;
- the volume of the parallelepiped with sides
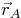 ,
,
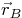 , and
, and 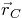 ;
;
- the angle between vector
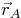 and the
and the 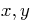 -plane.
-plane.
Use vector analysis only, including the appropriate vector products.
(Do not use trig, say.)
Solution.
- Background: Library LU decomposition subroutines are typically
intended for determinate square systems of equations. If you want to
study the possible solutions of indeterminate systems, you may want
to write your own LU decomposition subroutine.
Question: Given the matrix
- Reduce this matrix to echelon form, as defined in your notes.
Avoid fractions, but use only partial pivoting to achieve
that. Do not multiply the original equations by a non unit
factor.
- From the echelon matrix, find the null space.
- Show that a lower triangular square matrix
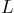 of multipliers
times the echelon matrix produces a partial pivoted version of
matrix
of multipliers
times the echelon matrix produces a partial pivoted version of
matrix 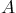 .
.
Use class procedures only.
Solution.
- Background: To analyze the stability of dynamical systems,
you may want to look at their potential energy under small
deflections, which is a quadratic form.
Question: Analyze the quadratic curve
using the class procedure of coordinate system rotation. Very, very
neatly draw the curve and rotated coordinates in the 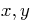 plane.
Clearly indicate all angles and relevant intercepts, with their
values.
plane.
Clearly indicate all angles and relevant intercepts, with their
values.
Solution.
![]() :
:
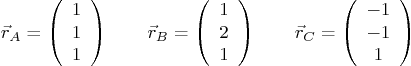
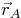 and
and
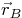 ;
;
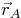 and
and
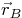 ;
;
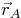 ,
,
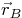 , and
, and 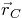 ;
;
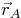 and the
and the  -plane.
-plane.
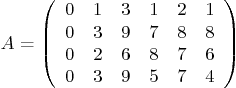
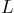 of multipliers
times the echelon matrix produces a partial pivoted version of
matrix
of multipliers
times the echelon matrix produces a partial pivoted version of
matrix 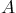 .
.