EML 5060 Analysis in Mechanical Engineering 12/12/14
Closed book Van Dommelen 10-12 noon
Solutions should be fully derived showing all intermediate
results, using class procedures. Show all reasoning. Bare
answers are absolutely not acceptable, because I will assume they come
from your calculator (or the math handbook, sometimes,) instead of
from you. You must state what result answers what part of the
question. Answer exactly what is asked; you do not get any credit for
making up your own questions and answering those. Use the stated
procedures. Give exact, fully simplified, answers where possible.
One book of mathematical tables, such as Schaum's Mathematical
Handbook, may be used, as well as a calculator, and a handwritten
letter-size formula sheet.
- Background: To understand the topology of a flow, and in
particular where the fluid goes, the behavior of the streamlines
near the stagnation points must be studied.
Question: The streamlines near a double stagnation point in
an ideal two-dimensional flow are given by
Solve this equation using the class procedure for this type of
equation. Neatly and accurately draw the solution lines for the
case that the appropriate integration constant is zero. Use a
different color for the solution lines, or fatten them.
Solution.
- Background: The Laplace transform is a primary way to
study the stability and evolution of linearized dynamical systems,
because it turns them into algebraic systems.
Question: Consider the response of the following frictionless
spring-mass system that experiences a forcing for a limited time:
Find the evolution using the Laplace transform. There may be no
funny functions in your answer; it should be phrased so that anyone
can understand it.
A table of Laplace transforms is attached. Everything not in this
table must be fully derived showing all reasoning. The convolution
theorem may only be used where it is absolutely unavoidable. Do not
use any complex numbers in your analysis (besides  .)
.)
Solution.
- Background: While nonlinear systems of differential
equations are usually not analytically solvable, their qualitative
behavior can be understood by analyzing their critical points (and
behavior at infinity).
Question: Consider the equation for a pendulum that experiences
both laminar and turbulent damping:
Write this equation as a first order system. Then explain why near
equilibrium, 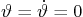 , small perturbations are
governed by
, small perturbations are
governed by
Solve the above linearized system using the class procedures for
first order systems. Draw the solution curves in the 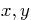 -plane
very neatly and quantitatively reasonably accurately. You should
have 2 examples of each different type of curve, or 1 if there is
just one curve of that type. Be sure to put an arrow in the
direction of motion on each curve. Make sure that you check your
algebra carefully. You do not get credit for making the wrong graph.
-plane
very neatly and quantitatively reasonably accurately. You should
have 2 examples of each different type of curve, or 1 if there is
just one curve of that type. Be sure to put an arrow in the
direction of motion on each curve. Make sure that you check your
algebra carefully. You do not get credit for making the wrong graph.
Finally, can we be confident that the shape of the solution lines of
the nonlinear system will be approximately the same, if we are close
enough to equilibrium? Why/why not?
Solution.
Table 1:
Properties of the Laplace Transform.
(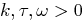 ,
,  )
)
|
|
![]() .)
.)