EML 5060 Analysis in Mechanical Engineering 11/8/06
Closed book Van Dommelen 11:50-12:40 pm

Solutions should be fully derived showing all intermediate results, using class procedures. Show all reasoning. Bare answers are absolutely not acceptable, because I will assume they come from your calculator (or the math handbook, sometimes,) instead of from you. You must state what result answers what part of the question if there is any ambiguity. Answer exactly what is asked; you do not get any credit for making up your own questions and answering those.

You must use the systematic procedures described in class, not mess around randomly until you get some answer. Do not take shortcuts. Some reminders: You need to reduce matrices completely to echelon form where appropriate to the question, (but not to row canonical if it would be inefficient for large matrices), using the procedure given in class, find the basis of the null spaces and orthonormalize eigenvectors using modified Gram-Schmidt where appropriate, etcetera. Do not throw away zero rows in Gaussian elimination. Coordinate transformations must be found using transformation matrices only. Coordinate transformations for symmetric matrices must be orthonormal. Inverses of unitary matrices must be found by transposing. Principal axes and principal values must be found as eigenvalue problems using class procedures. Polynomials of matrices above degree 2 must be found using diagonalization. Quadratic forms must be reduced using class procedures.

One book of mathematical tables, such as Schaum's Mathematical Handbook, may be used, as well as a calculator, and a handwritten letter-size formula sheet.

1. Background: Statically undetermined structures can have internal stress fields of varying nature. One way to see the different possible fields is to write finite element equations for the structure and then examine the basis of the null space.

   Question: Find a basis of the null space of the matrix
   

   $$\left( \begin{array}{rrrrr} 3 & 6 & 9 & 12 & 15 \\ 2 & 4 & 4 & 4 & 4 \\ -2 & -4 & -3 & -2 & -1 \end{array} \right)$$
   
   

   Solution.

2. Background: The eigenvalues of the $4\times4$ Dirac matrix
   
   $$\left( \begin{array}{rrrr} 1 & 0 & 0 & p \\ 0 & 1 & p & 0 \\ 0 & p & -1 & 0 \\ p & 0 & 0 & -1 \end{array} \right)$$
   
   
   describe the possible energies of an electron moving in free space, where $p$ is the scaled linear momentum of the electron.

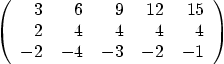
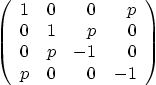
   Question: Find the eigenvalues of the matrix above. Do not use any Gaussian elimination. Without solving for the eigenvectors, what can you say about the diagonalizability of the Dirac matrix and why?

   Solution.

3. Background: The potential energy of a system of two masses aligned in an array using springs is
   
   $$q = 7 x^2 -12 xy + 23 y^2$$
   
   
   where $x$ is the displacement of the first mass, and $y$ the one of the second.

   Question: Find the approriate new unknowns $x'$ and $y'$ in terms of which $q$ above can be written without an $x'y'$ term. Graphically show the relationship between the coordinates $x,y$ and $x',y'$.

   Solution.